CLASSIC TECHNIQUES 
Long-Term Fibonacci
Support And Resistance 
by Kevin W. Murphy
Here's a historical review of the major swings in the stock market and the Fibonacci relationships.
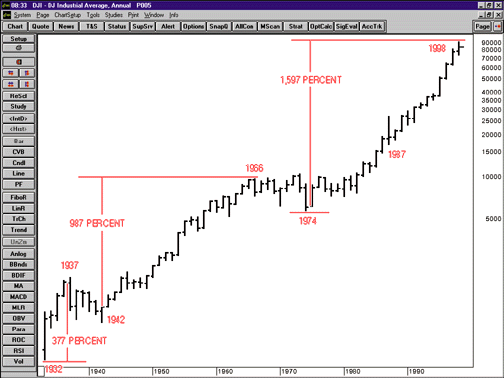
According to long-term Fibonacci? support and resistance levels in the Dow Jones Industrial Average (DJIA), we are approaching a notable resistance level in the stock market. Many books have been written on the Fibonacci sequence and its many mathematical relationships; this article will not delve into those in any great detail. For those who are unfamiliar with the Fibonacci sequence, however, I will briefly discuss its basis and a few of its mathematical relationships and how they are relevant to investors.

Leonardo of Pisa, a 13th-century mathematician, illustrated what would later be known as the Fibonacci sequence in his work Liber Abacci, although its mathematical relationships were not detailed until much later. The Fibonacci sequence is an additive sequence in which each number is the sum of the two numbers preceding it. Beginning the sequence with 1, it progresses thus: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 ... on to infinity.

As the sequence continues to infinity, the ratio of each number to its preceding number approaches 1.61803398 (also known as the golden ratio). Because it is an additive sequence, any two numbers can be used to begin the sequence and added together to produce a third and so on. Whatever two numbers are used to begin the sequence, the resulting ratio between each preceding number will ultimately approach 1.61803398. Within the sequence, the mathematical relationships of Fibonacci numbers are depicted: the ratio of any number to the following number in the sequence is 0.618, which is the inverse of 1.618. The ratio between alternate numbers is 3.618 or its inverse, 0.382. Moreover, 0.382 plus 0.618 equal 1 and (0.618)(0.618) equals 0.382.

The mathematics of the Fibonacci sequence are well-documented and you may want to test out a few numbers for yourself. For the purpose of our analysis, we are now going to apply the mathematics of Fibonacci to the Dow Jones Industrial Average (DJIA) dating back to the 1930s. Before we do, however, we must introduce the first person to apply Fibonacci mathematics to the stock market, Ralph Nelson Elliott, who devised the Elliott wave theory. Elliott described how markets moved in his wave theory, and he showed how Fibonacci mathematics can be applied to these moves. Although I will not discuss Elliott's wave theory in detail, there are two key tenets of his theory that I will apply in this article, price and time.
 
 

FIGURE 1: DJIA, 1942-66. Here's an increase of 987% between 1942 and 1966. Although we know the increase in the price of the Dow industrials was somewhere between 971% and 980% on a print basis, as in the case of the 1932 to 1937 advance, we can only approximate the exact print level.
Kevin Murphy began investing in 1972 and entered the financial industry as a broker in 1990. During his first years as a professional, he ranked in the top 10 nationally in the CNBC/FNNand USAToday National Investment Challenge professional options division from 1990 to 1992, with returns ranging from 500 to 800%. In 1993, he won first place with a return of 1,978% over a period of three months. He currently manages private money and teaches Elliott wave and Gann seminars throughout the US. He can be reached via E-mail at kwmurphy@ mindspring.com.
 
 
Excerpted from an article originally published in the October 1998 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 1998, Technical Analysis, Inc.
Return to October 1998 Contents