More Responsive Moving Averages
by Joe Sharp, Ph.D.
Traders are resigned to moving averages being behind the price action, but that needn't always be the case. Here's an algebraic technique to make your averages more responsive to price movement -- and a better aid in decision-making.
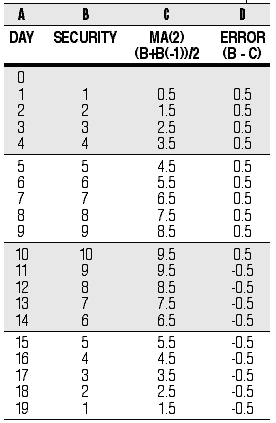
FIGURE 1: LAG IN AVERAGES. Whether rising or falling, a simple moving average never catches up with a trending price. This table shows the consistent error inherent in a simple moving average.
You can fix that. I'll show you a corrected moving average that can follow trends accurately. You'll have to endure a little math to get the idea, or you can use the spreadsheet I've provided. (To download, check the "References" section at the end of this article for the location on the STOCKS & COMMODITIES Website.)
THE OLD WAY
First, I want to show you a simple example of a problem that's easy to calculate by hand. It can be seen in the spreadsheet in Figure 1, and I'm using it here just to introduce the problem and suggest how to fix it.
Start the column marked "Day" at day zero and run it downward to 19. Then, starting at day 1, give the security value column values from one up to 10 and back down to one.
Compute a simple two-day moving average by hand. The first value, for example, in column C is (1+0)/2 = 0.5. On day 2, it's (2+1)/2 = 1.5, and so on.
The Error column is the difference between the security's price and the average. For the first line, that's 1 - 0.5 = 0.5. The column shows that the average will never be able to catch up with the rising and falling ramp; it will always lag behind the correct value of the underlying security by half the change in the period included in the average. Similarly, simple moving averages lag behind falling security values.
OF THE FIRST ORDER
Since a simple moving average uses only one total of the prices used, it's referred to as a first-order model. That single total can only model the average value of a security over a specific period. It finds the best curve through the numbers, but it can't estimate the slope -- the rate of rise or fall -- of the price movement, so it can't catch up with a rising or falling value of a security.
FIXING THINGS
Back in the 1950s, mathematician Robert G. Brown dealt with lag in estimating inventories. His solution applies to our problems as well. To fix the average, you must add a second total to the equation, a total that reflects the slope of the price rise and fall. At first glance, adding a second total may appear complicated, but you'll see how easy it is to use.
To get at the value of the slope is a complicated derivation (see sidebar, "Computing the modified moving average," for the formula), but the idea is straightforward. First, you compute the sum of a weighted set of prices to use in the computation of the slope value. These weights give far more weight to recent prices than they do to older prices. The weighting is so extreme that it actually subtracts older values! Once you've computed the sum (let's call it S), use the formula to compute the modified moving average.
If you try this with a two-day average, you can do the math by hand. The spreadsheet shows how to do it for three- and four-day averages as well.
Joe Sharp teaches computer science at the Rochester branch of the University of Minnesota and can be reached at sharpjoe@home.com. His digital signal processing experience is now being applied to security analysis and selection.
Excerpted from an article originally published in the January 2000 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 1999, Technical Analysis, Inc.
Return to January 2000 Contents