TRADING TECHNIQUES
Optimal Detrending
by John F. Ehlers
Did you know that a detrended signal, combined with an optimum smoothing filter, can produce an extremely responsive oscillator-type indicator that catches every cyclic turn as it happens? It's true! Here are the details.
There must be a jillion ways to detrend price data, and a good chunk of them have already been explored in print. Given that, I had to have a new and significant approach to the subject -- and here it is. I discovered that a detrended signal, combined with an optimum smoothing filter, can produce an extremely responsive oscillator-type indicator.
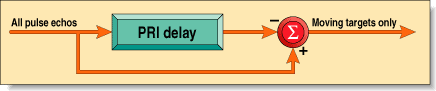
FIGURE 1: PULSE CANCELLER ELIMINATES FIXED TARGETS. Many radar systems, such as those used in air traffic control, are only used in relation to moving targets. These radars use a circuit called moving target indicator (MTI). There are several ways to implement MTI, but the simplest way is to use the echo from a fixed target due to the previous pulse to cancel the echo from that same target from the current pulse. HereÕs a block diagram showing how this is accomplished.
I borrowed the concept of this new detrending approach for the markets from radar circuit designs, so to understand how it works, let's first take a look at how radar works.
To refresh your memory, radar (which is an acronym, sort of, for radio detecting and ranging) works by transmitting a high-powered radio-frequency (RF) pulse and listening for the return echoes from various targets. RF energy travels at the speed of light, and so the round-trip time for an echo comes out to 12.4 microseconds per mile. The distance of the target from the transmitter is determined by measuring the time it takes for the echo to return. After sufficient time has elapsed so no more echoes are expected, the radar transmits another pulse. The process is repeated, and the time between pulses is referred to as the pulse repetition interval (PRI).
Many radar systems, such as those used in air traffic control, are only used in relation to moving targets; these radars use a circuit called a moving target indicator (MTI). There are several ways to implement MTI, but the simplest way is to use the previous echo from a fixed target to cancel out the current echo from that same target. Figure 1 is a block diagram that shows how this cancellation is accomplished. The delay line delays the echo from the previous pulse by exactly one pulse repetition interval. Thus, pulses from fixed targets appear at exactly the same time and are canceled out, whereas pulses from moving targets do not occur at exactly the same time from pulse to pulse, and therefore are not.
PULSE, PRICE, AND INTERVAL
So how does this relate to detrending? Simple. Like the pulses of radar, if we subtract the price N bars ago from the current price, the constant components of the prices cancel each other out. This N-bar momentum function -- which is the subtraction of price N bars ago -- takes out the trend because the trends are the nearly constant cycle components of price (they change, so they cannot be exactly constant). And like the pulses of radar, trends are eliminated by removing -- canceling out -- the previous price from the current one by using the N-day momentum function. So the question becomes: how are the cycle components, the variable parts of the simple model, affected by the momentum function?
John F. Ehlers, Box 1901, Goleta, CA 93116, is an electrical engineer working in electronic research and development and has been a private trader since 1978. He is a pioneer in introducing maximum entropy spectrum analysis to technical traders through his MESA software. He may be reached at 805 969-6478, or via his Website at https://www.mesa-systems.com.
Excerpted from an article originally published in the July 2000 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 2000, Technical Analysis, Inc.
Return to July 2000 Contents