VOLUME INDICATORS
Editor,
It was with considerable interest that I recently read the interview with David Vomund in the October 1999 S&C. He brought to mind what I felt was a balanced view of market efficiency. He also whetted my appetite for volume indicators. I already use Marc Chaikin's money flow indicator in the Australian market, without a great deal of success, and I am interested in the volume accumulation percent indicator. However, as Vomund does not mention how this indicator is calculated, and I have no other references to it, I wonder if you can enlighten me?
Trevor T. Bestow, via e-mail
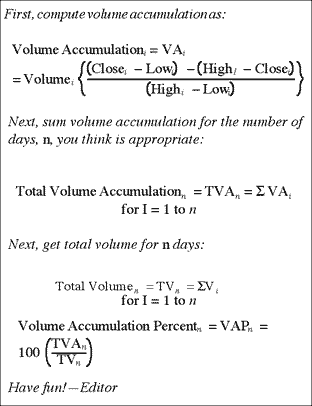
CANDLE PATTERNS
Editor,
In the January 2001 Letters to S&C, reader Dejan Milenkovic mentions that upmoves end with a hanging man candle pattern and downmoves with a hammer pattern. He is correct. This is a serious shortcoming often overlooked in Japanese candle pattern analysis: You cannot have a bearish reversal candle pattern in a downtrend, only in an uptrend. Similarly, you cannot have a bullish reversal pattern in an uptrend. Reversal patterns call a reverse of the very trend that helped identify them in the first place.
By the way, John, I didn't think anyone could replace Thom Hartle as editor of S&C, but you are doing a superb job!
Greg Morris,
via e-mail
MurphyMorris, Inc.
Obviously, you are correct on all points. -- Editor
CANDLESTICKS REVISITED
Editor,
The article "Coding Candlesticks" in your November 1999 issue contains an interesting approach to quantifying candlesticks. But after a second reading, my initial enthusiasm cooled off by quite a number of degrees. It seems to me that the author has made a fundamental error insofar as he confuses coding with valuating or weighing a candlestick.
The proposed "code" is a seven-bit number in which the main characteristics of any single candlestick can be recorded -- that is, encoded. Although Viktor Likhovidov explains the coding scheme, it can only be the starting point for the part that matters: the valuation. Here, Likhovidov just tells us that "the sense" of the coding scheme consists of assigning the highest value to the most bullish candlesticks and gives lots of examples.
In assigning weights directly to these binary codes, he runs into difficulties. For example, different codes are assigned to white versus black bodies (long white = "11," long black = "00"), although color already has a value of its own: the seventh bit.
The most serious problem, however, arises out of the respective positions of the upper and lower shadows in the code; a long upper shadow is assigned a value of 12, a long lower shadow gets zero. This is where I get confused. Evidently, lower shadows are more bearish than their upper counterparts. Are shadows generally bearish?
I disagree. An upper shadow means the bulls tried to push prices up but didn't succeed, so it is bearish; a lower shadow means the bears had a try but got their noses bashed, and it should be considered bullish. This commonsense interpretation is confirmed by Steve Nison in his book Beyond Candlesticks.
This brings up the problem of valuation. For instance, a hammer appears in a downtrend, but a hanging man (the same candlestick) appears in an uptrend. This is a problem that remains inherently unsolvable with a one-period indicator. You must consider the context when valuing candlesticks.
I'm sorry to say that I'm not yet done with my criticisms. I also have to object to the method used to compute the values for the long, middle, and short thresholds. In the article, Bollinger Bands around a moving average are used. These are, as Likhovidov correctly notes, computed on the basis of the "standard normal distribution." That's certainly not what we have here. Candlestick lengths have a theoretical upper limit of infinity and a -- very practical -- lower limit of zero.
This means we are dealing with a log-normal distribution that is skewed to the left. Thus, using 0.x standard deviations below and above the average value results in uneven bites taken from the total spectrum.
At a more basic level, this raises a question about the coding scheme per se. Here, we have a complicated method that is used to divide the spectrum of possible values into just three categories: small, middle, and long. The fourth value, zero, is added to account for dojis and so forth. I believe this is too stringent. Very small values should be counted as nil, too. So for them, a fourth category is needed. Maybe we would get better results using 10% percentiles.
Why use an artificial subdivision of values at all? Using the actual values of bodies and shadows, multiply the body's value with a factor x, add the lower shadow, subtract the upper shadow, and there is our indicator.
Jan Willem E. Roberts
Munich, Germany
Jan W.E. Roberts's letter stimulated Likhovidov to return to the subject
and elaborate. See his article "Coding Candlesticks (II)" in
this issue. Roberts's letter included many other ideas that I edited out
for brevity. I hope he'll write them up in a separate article. -- Editor
FORMULAS AND SPREADSHEETS
Editor,
I just read Arthur Merrill's letter in the December 2000 issue, in which he discussed the problem of articles that do not provide formulas or an Excel spreadsheet. I support the recommendations he made in his letter. I was frustrated by John Ehlers's article on the squelch indicator because it seemed to be a valuable indicator, but I could not check it out because of the lack of basic formulas or an Excel spreadsheet. As a longtime subscriber to your magazine, I have often had this frustrating experience. I suggest that basic formulas and a spreadsheet example be requirements of having an article accepted for publication.
Paul D. Baba, via e-mail
San Carlos, CA
Okay! Okay! We'll write spreadsheets for you guys! But we've got time constraints, you know! -- Editor
EASYLANGUAGE
Editor,
Could you publish SuperCharts EasyLanguage for the Andrews pitchfork featured in your article in the December 2000 issue?
Kent Siegrist, via e-mail
Please contact TradeStation Technologies, Inc. (formerly Omega Research, Inc.), for code for use in their products; we don't specialize in writing EasyLanguage. Check also the TradeStation website at www.TradeStation.com for already-posted code, since they publish quite a lot of custom code there.
In S&C, we try to provide the basic math, spreadsheet, or logic for a concept, and readers may implement it in whatever product they happen to use. We sometimes include the code for MetaStock or TradeStation if the article's author works in that program and can provide it.
If TradeStation Technologies cannot provide this particular code and
if the Andrews pitchfork is not a built-in charting feature of your program,
you might try looking for third-party suppliers of custom code.-- Editor
NORMALIZING THE GAPO
Editor,
After reading about the Gapo index in the January 2001 issue ("Gopalakrishnan Range Index"), I realized that it needed to be normalized to the underlying securities' base price to have any interpretable meaning. For example, if security A has just closed at 10,000 and its max-min for the past five days is 500, then the Gapo value will be log(500)/log(5) or 3.86. In contrast, if security B just closed at 10 and its max-min for the past five days is 0.5, the Gapo value will be log(0.5)/log(5) or -0.43.
The interpretation in the article would lead one to think that security A is dramatically more volatile and erratic than security B, even though they both show the identical percentage price change (range of 5% over the past five days). Comparing markets based on their relative volatility and consistency of price behavior is a worthy goal. Unfortunately, unless normalized for each security's base price, the Gapo does not accomplish this task. A more tried and true measurement would be to compute the traditional historical volatility for each security and use that to compare each security's relative "erratic behavior."
Joseph M. Fisher, M.D., Ph.D., via e-mail
San Carlos, CA
Sounds like a good follow-up article. See also the response to the next
letter. -- Editor
MORE ON NORMALIZATION
Editor,
Unless I've overlooked something obvious in the formulation of the Gapo index in the January 2001 issue, a one-point spread taken over five days in a $10 stock would have the same implication as a one-point spread in a $200 stock. If my interpretation is correct, the index is of questionable use. On the other hand, if one were to determine an average price for the issue (or index or commodity) for the period of interest, such as five, 10, or 21 days, and divide that value by the high-low range (or the inverse), one would be on the way to determining relative (normalized) volatilities that are comparable. I have developed and used similar methods for a number of years.
M.G. Boobar, via e-mail
We think both thoughts are worth pursuing and invite an article on either subject -- or both. -- Editor
FIBONACCI RATIOS
Editor,
I read Rudy Teseo's interesting article, "The Gartley Setup," in the January 2001 S&C. This pattern seems to be the same as that shown in Larry Pesavento's Fibonacci Ratios With Pattern Recognition. Regarding this pattern structure (named Gartley 222), the book writes at point 6: "If point X is exceeded the trend will continue to move down to at least 1.27 or 1.618 of the X to A move."
How does this reconcile with what is written in Teseo's article? Figure 1 clearly shows that the CD leg can be 1.27/1.618 of the BC leg, and that in any case all the retracement AD must not be greater than 0.786 of XA (that is, D must not be less than point X). I think that some misunderstanding is occurring with this pattern. Would it be possible to get some clarification from Rudy Teseo?
Guglielmo Marco, via e-mail
Carmagnola, Italy
Rudy Teseo replies:
I have not read Larry Pesavento's book and have no idea what coverage he has given to all the possible harmonic patterns. However, my article only applied to the ideal bullish Gartley. What you are referring to, I believe, is the bullish butterfly. In this pattern, the ratios are somewhat different. The AB ratio is 0.786, the BC ratio is 0.618./0.786, and the CD ratio is 1.27/1.618. Again, these are ideal figures. I trust this answers your question. Thanks for your interest.
ASTROLOGY AND THE MARKETS
Editor,
It was a pleasure to read Arthur Merrill's letter in the December 2000 issue regarding his study of the relationship between full moons and the Dow Jones Industrial Averages (DJIA). I have great regard for Merrill's work, and I still treasure an autographed copy of his classic Filtered Waves, Basic Theory.
First, if one really wants to know whether there is a correlation between astrology and financial markets, then one must attempt to understand the nature of astrology. It is not a study that lends itself well to empirical science or statistics, which will almost immediately cause a skeptic to assume that the method is of little value.
Merrill concurs with Brooks Rimes, who questioned the place of astrology in technical analysis in a prior letter. He states that he tries to keep an open mind to the subject, but to date has seen no evidence that demonstrates the validity of astrology as a market analysis tool. As one of the pioneers in this field, I would like to comment.
Merrill's full-moon study concurs with quantitative studies I have conducted on solar and lunar eclipses, which are considered even more potent to most proponents of astrology than full moons (The International Astrologer Journal, Spring 1998, Volume XXVII, No. 2). Again, there is no evidence of a statistical correlation to crests, troughs, or price direction in the DJIA when plotted anywhere from zero to five days to either side of either eclipse. The results did not disturb me, for I had observed as much over the past 20 years. However, I was concerned because so many financial astrologers frequently claimed that there was a correlation and implied that it was one of the most important astrological indicators, yet they never cited evidence or even anecdotal examples to back up these claims.
Here is where knowledge of astrology can be invaluable to one who wants to determine whether there is any correlation to financial markets. Most astrologers understand that lunar cycles are relatively mild in their correlation to cycles of human activity in comparison to planetary cycles. Yet most academic researchers try to prove or disprove astrology (especially in financial markets) through statistical studies involving new or full moons.
A new moon is simply a moment in time where the moon and sun appear to be in alignment, as seen from the Earth. It occurs about every 29 days. It is not a rare event. Likewise, a full moon occurs approximately every 29 days, when the sun and moon are on opposite sides of the Earth. Yet planets appear together or in opposition to one another too, and far less frequently, which would seem to be a more intriguing basis for a study than something so transitory as the moon in its orbit around the Earth.
My own quantitative studies on these astronomical events, as published in several books, suggest a far stronger correlation to financial markets than either new or full moons, or solar or lunar eclipses. I would be more than happy to send Arthur Merrill a copy of these published studies related to gold, silver, or US stock market indices if he were interested.
The problem with doing any kind of statistical study to validate astrology lies in the mechanics of both astrology and market activity. For instance, specific astrological signatures rarely correlate with only a crest or a trough in a given financial market. The theory behind astrology is that it marks a change in collective psychology or investor sentiment. For example, in one instance, a sun opposite Jupiter (which occurs about once every 13 months) might correspond to a multi-month crest in US stocks, but in the next instance, it might correlate to a multi-month trough. The point is that certain astrological signatures (but not all) have a correlation to market reversals, or a change in investor sentiment. How long that change will last depends upon a multitude of other factors, both astrological and mundane, such as the technical or cyclical condition of the market.
The matter is compounded by the fact that single astrological signatures rarely occur. They are often present with other signatures that occur nearby in time. For instance, the sun may oppose Jupiter every 13 months. But in one year, Mars may conjunct Uranus two days earlier, and in another year, Venus may conjunct Mars one day later. In another year, both of these signatures (or others) may occur within the same week, while in yet another year, no other significant signatures occur nearby. Merrill might find the same thing even in his full-moon study. That is, those full-moon dates in which stocks seem to respond sharply may have coincided with periods in which other geocosmic signatures were occurring within a day or two.
By the way, I noticed that Merrill's study cites 60 full moons between 1992 and 1999. Since there are 13 full moons per year, this suggests about 30 instances are missing. Was this perhaps due to the fact that he did not consider full moons that occurred over weekends? Just a question in the spirit of research, as I don't think the results would have changed significantly anyway, due to my belief that lunations have very little correspondence to trend changes in US stock indices.
The mechanics of financial market prices also present challenges to a proper statistics study. Let's say one wishes to analyze the dates from which 4% or greater filtered waves are defined (to use one of Merrill's technical tools, which I use to conduct studies relating astrology to financial markets). Let's say there is a crest from which prices decline more than 4%. However, before the greater part of that decline commences, the market trades for a week or so in congestion, forming a double top one week later. The second crest is just a tick below the first crest. Which crest do you use? The first one, which records the actual high tick, or the second one, which commenced the more severe decline? In attempting any kind of statistical research involving any market timing indicator (that is essentially what astrology is), one has to define a variety of criteria to be used in order to create results that are useful to actual traders or investors.
I would like to thank Arthur Merrill -- and Brooks Rimes -- for opening up this discussion on astrology and financial markets. Unlike so many authorities on financial markets, Merrill at least tries to keep an open mind on the subject. That is greatly appreciated by serious market students like myself. Most scientific people tend not to give any credence to astrology for only one illogical, unscientific reason: it shouldn't work, therefore it doesn't work.
Raymond Merriman, CTA, CAP
Editor, The MMA Cycles Report
West Bloomfield, MI
Rudy Teseo replies:
Thanks to all the readers who contributed to our discussion of astrology and trading, since it was prompted by our review of Ganntrader 3.0 in the July 2000 issue of S&C. -- Editor
WORTHLESS OPTIONS
Editor,
I would like to respond to the article "How Many Options Actually Expire Worthless?" by Lawrence McMillan in the January 2001 issue. I am quite surprised by the percentages mentioned. I am active in the European market and have done significant research, and I have a different conclusion.
I have several years of data for the the Amsterdam general index (AEX) -- the Dutch Dow, if you will. For example, the bottom chart on https://www.night-trading.com/openinterest/oi_aex.html shows the percentage of options that will expire worthless given the value of the AEX, if expiration were today. The number is above 60% with the current index of around 630. Historically, it's around 70% on expiration. This also applies to individual stocks. I'm surprised that the figures for Chicago are so different from those for Amsterdam.
The chart itself is quite interesting. The price tends to go to the top of the chart, where the percentage is the highest, and thus contains some predictive value toward the price goal at expiration.
John Phoenix, via e-mail
AUTOMATIC TRADING SYSTEM
Editor,
Has anyone ever demonstrated or sold a trading system that can be set to operate on full automatic -- that is, make real trades with real money for the investor, without constant supervision and without the investor having to okay each trade? Are there any systems like this currently available, or any being discussed that you can talk about?
Larry Burford, via e-mail
Yes, some brokerage houses integrate trading systems with their brokerage services. Two examples are Zap Futures and Lind-Waldock -- Editor