TRADING TECHNIQUES
Phasors Set On "New"
MESA Adaptive Moving Averages
by John F. Ehlers
What if you combined the power of maximum entropy spectral analysis with the Hilbert transform's ability to discern phase change?
The Mesa adaptive moving average (MAMA) adapts to price movement in a new and unique way. The adaptation is based on the rate change of phase as measured by the Hilbert transform discriminator I described in my December 2000 S&C article. In that article I derived the Hilbert transform, which generates the real and imaginary components from the analytical price waveform. The arctangent of the ratio of the imaginary component to the real one is the phase angle at a given point in time. Since the summation of the delta phases from bar to bar reaches 360 degrees, completing a cycle, the Hilbert discriminator computes the dominant cycle on the basis of the average phase differential.
The advantage of this method of adaptation is that it features a fast
attack average and a slow decay average so that the composite average rapidly
ratchets behind price changes and holds the average value until the next
ratchet occurs. Ratcheting refers to the short time constant upon command
that allows the adaptive moving average to approach price value; thereafter,
the moving average moves slowly with price until the next command it receives
to apply the faster moving average. The ratcheting gives the adaptive moving
average a stairstep appearance. The combination of fast attack and slow
decay is like an electronic sample and hold circuit -- that is, the adaptive
moving average rapidly moves toward the current price upon command and
essentially holds that value, or slowly follows price, until the next update
command arrives.
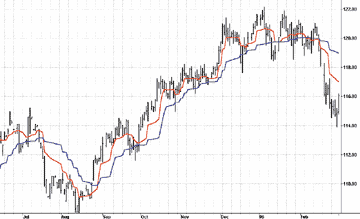
FIGURE 1: MAMA/FAMA. MAMA (red) tracks price tightly. The crossover of MAMA and FAMA is a good trend signal.
The action of MAMA is shown in Figure 1. Since the average fallback is slow, I can build trading systems that are virtually free of whipsaw trades.
The starting point for MAMA is a conventional exponential moving average
(EMA). The equation for an EMA is written as:
Ema = a*Price + (1 - a)*Ema[1]
where a is less than 1
In plain English, the EMA is created by taking a fraction of the current
price and adding one minus that fraction times the previous value of the
EMA. The larger the value of a (alpha), the more responsive the EMA becomes
to the current price. Conversely, if a becomes smaller, the EMA is more
dependent on previous values of the average rather than the current price.
Therefore, one way to make an EMA adaptive is to vary the value of a according
to some independent parameter. The Kaufman adaptive moving average (KAMA)
and the variable index dynamic average (VIDYA) introduced by Tushar Chande
both use the variation in prices, or volatility, as the basis of their
adaptations.
...Continued in the September 2001 issue of Technical Analysis of STOCKS & COMMODITIES
John Ehlers is president of Mesa Software and a frequent contributor to STOCKS & COMMODITIES. He pioneered the Mesa algorithm for measuring market cycles. This article was adapted from Rocket Science For Traders from John Wiley & Sons. Ehlers may be reached via his website at www.mesasoftware.com.
Excerpted from an article originally published in the September 2001 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 2001, Technical Analysis, Inc.