Harmonics In The Markets
Fourier Transforms As An Aid To Decision-Making
Traditionally, technical analysis has been used to detect and interpret patterns in past security prices to provide insight into future price movement. This, in turn, has lured researchers to try to beat the markets consistently, using a range of techniques varying from mathematics, physics, and economics to psychology. In this article, I will focus on the use of Fourier transforms together with technical analysis in making trading decisions.Is exiting a portion of your trade before your profit target is hit a viable strategy?
Fourier transforms
The application of Fourier transforms has been well established in
fields like digital signal processing (DSP), medical diagnostics, image
processing, the media, and so on. The Fourier transform breaks up a signal
from the time domain to a frequency domain, characterizing signals and
letting you see order where there appeared to be none. For this article
I used the transform to convert raw data into useful information to aid
in making trading decisions.
Many technical analysis indicators seem to work well for specific kinds of patterns. Unfortunately, there are no indicators that can take into account all of the possible characteristics that a price series can exhibit. I will show you how to incorporate stock price volatility so your indicators can adapt accordingly.
Apparently, stock price movement depends upon a number of known and unknown variables with a complex order of correlations existing among them. I will start by providing a brief overview of technical analysis and Fourier transforms, then state the problem context, followed by a brief description of the deficiencies of technical analysis, and finally describe the possibilities found by exploring Fourier transforms, frequency analysis, and inverse transformations.
Technical indicators
Although numerous indicators are available, I will focus on the effective
usage of the two most significant indicator categories: averages and oscillators.
Averages like the moving average and moving average convergence/divergence
(Macd) are lagging indicators that take previous values into account to
categorize the present. They do not tell us anything about the upcoming
changes; hence, they work best when prices move in relatively long trends.
Oscillators like stochastics and Williams' %R are leading indicators that
assume price swings are bound to happen when a security becomes overbought
or oversold. Thus, they work best in horizontal yet volatile price patterns.
Fourier transforms
Any continuous signal (that is, a signal that has only one value at
any instant in time) can be represented by the sum of sine waves of varying
frequency, amplitude, and phase. In the context of stock prices, the set
of price values over a period of time becomes the signal. Two terms that
commonly arise in discussions on frequency analysis are time domain and
frequency domain. A time domain signal is a function of time, written as
f(t), and a frequency domain signal, written as F(w).
Among waves of different frequencies, the lowest frequency depends upon the period taken for the input signal. That is, for a time period of size N, the lowest frequency would be 1/N. Any frequency lower than this cannot be fit, and goes into zero-frequency DC offset.
In order to accurately find the composite frequencies, the mean (DC offset) should be removed from the input signal. The subsequent higher frequencies would be higher-order harmonics (2/N, 3/N...up to 1/2) of the lowest frequency (fundamental wave).
The transformation from the time domain to frequency domain is called a forward transformation. The reverse is called an inverse or backward transformation. The forward Fourier transform of an array X of size n computes an array Y:
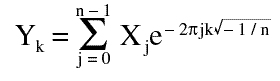 Equation
1
Equation
1
where the k output corresponds to frequency k/n.
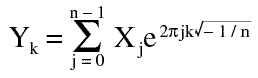 Equation
2
Equation
2
Since there are no coefficients prior to summation, performing a forward followed by an inverse transformation would scale the output by a factor of n. The formulas mentioned here describe a nonnormalized transformation.
For the purposes of technical analysis, it does not matter whether the
computation is done on normalized or nonnormalized input, since it focuses
on the pattern and not the absolute values.
...Continued in the February issue of Technical Analysis of STOCKS & COMMODITIES
Excerpted from an article originally published in the February 2005 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 2005, Technical Analysis, Inc.
Return to February 2005 Contents