Recognize Your Mistakes
Developing Discipline With Daily Debriefing
by Van K. Tharp, PhD
It's easier to design a system that will produce returns of 100% than it is to trade the system to get those results. Here's why.
IT is easy to design a system that will produce annual returns of 100% or more. Trading the system so you will get those returns is not so easy. Here's why it's easy to develop such a system, why it's so difficult to get those returns, and how to fix the problem.
IN TERMS OF R-MULTIPLES
First, let's start thinking about your trading results in terms of multiples of your initial risk (R-multiples for short). A key of trading success is that you must have a predetermined exit before you enter into a trade that represents your worst-case risk. Let's look at a few examples.
Suppose you decide to buy a stock at $25 and that you'll sell it if it drops 10% to $22.50. Your risk is $2.50 per share in this case. Suppose you decide to risk $1,000 in this trade. That means you can buy 400 shares of stock (that is, divide your total risk of $1,000 by your per-share risk of $2.50 and you get 400 shares). You would be buying $10,000 worth of stocks (400 x $25), but your initial risk would only be $1,000.
Suppose you have a $100,000 portfolio. Your risk for that position would be just 1%. Further, if your risk was 10% of the value of the stock, you could buy 10 different positions, each with 1% risk, to be fully invested. Suppose you had 10 such positions, with the results you see in Figure 1.
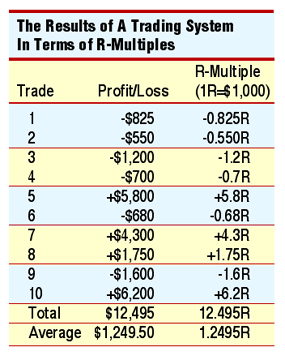
FIGURE 1: RESULTS IN TERMS OF R-MULTIPLES. If your risk were 10% of the value of the stock, to be fully invested in this hypothetical $100,000 portfolio, you would have to have 10 different positions, each with a 1% risk. In this system the expectancy is 1.2495.
The average R-multiple produced by the system is what I call the expectancy of the system. If your sample is large enough (and in our case 10 samples isn't), then your expectancy will tell you what you can expect per trade on the average over many trades.
Say that your expectancy over 100 trades is 1.2R and your system produces about 75 trades per year. Under those conditions, you might expect to make about 90R (that is, 75 multiplied by 1.2R = 90R) per year. And if you risked 1% of your total current equity on each trade, then you could easily make 100% per year.
Some might argue this is stretching things. For example, 90R is the average return you might get, but half the time the return will be better and half the time the return will be worse - 90R per year is a reasonable result for a good system, and there are many systems with much better results. The bottom line? A system that could deliver a return of 100% per year is not that difficult to design.
It is easy to design a system to make 100%, once you starting thinking
in terms of R-multiples, because a 10R gain means you only have to make
10 times your risk, not 10 times your investment. Thus, most people can
develop systems that make large R-multiple gains quite frequently. However,
even when they have developed such a system, most people cannot make 100%.
...Continued in the January issue of Technical Analysis of STOCKS
& COMMODITIES
Excerpted from an article originally published in the January 2007
issue of Technical Analysis of STOCKS & COMMODITIES magazine.
All rights reserved. © Copyright 2006, Technical Analysis,
Inc.
Return to January 2007 Contents