GO BACK
TRADESTATION: MEASURING CYCLE PERIODS
John Ehlers' article in this issue, "Measuring Cycle Periods," describes
the use of bandpass filters to estimate the length, in bars, of the currently
dominant price cycle. In the article, Ehlers presents two indicators and
also proposes a trading strategy.
Here, we'll provide EasyLanguage code for the indicators EhlersSpectrum
and EhlersDominantCycle. The strategy is called "EhlersBandPassStrat."
A sample chart implementing the indicators is shown in Figure 1.
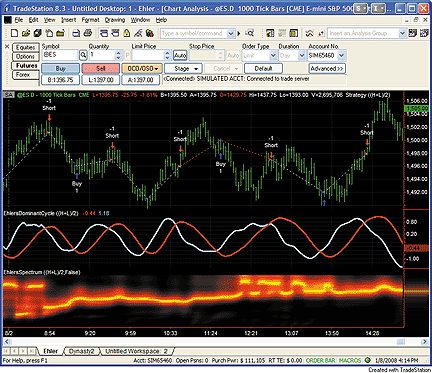
FIGURE 1: TRADESTATION, EHLERS' SPECTRUM INDICATOR AND DOMINANT CYCLE
INDICATOR. Here are Ehlers' indicators applied to a 1,000-tick chart
of the continuous S&P 500 emini futures contract (day session).
To download the EasyLanguage code for this study, go to the Support
Center at TradeStation.com. Search for the file "Ehlers Cycle Measurement.eld."
TradeStation does not endorse or recommend any particular strategy.
Indicator: EhlersSpectrum
inputs:
Price( MedianPrice ),
ShowDC( false ) ;
variables:
alpha1( 0 ),
alpha1Plus1( 0 ),
Log10( 0 ),
HP( 0 ),
SmoothHP( 0 ),
EhlersDelta( 0.1 ),
EhlersBeta( 0 ),
Cos720Delta( 0 ),
EhlersGamma( 0 ),
alpha( 0 ),
OneMinusAlpha( 0 ),
OnePlusAlpha( 0 ),
N( 0 ),
TwoPi( 6.2831854 ),
MaxAmpl( 0 ),
Num( 0 ),
Denom( 0 ),
DC( 0 ),
DomCyc( 0 ),
Cos720DeltaDom( 0 ),
CycleLine1( 0 ),
CycleLine2( 0 ),
Color1( 0 ),
Color2( 0 ),
PlotColor( 0 ) ;
arrays:
EhlersI[50]( 0 ),
OldI[50]( 0 ),
OlderI[50]( 0 ),
Q[50]( 0 ),
OldQ[50]( 0 ),
OlderQ[50]( 0 ),
Real[50]( 0 ),
OldReal[50]( 0 ),
OlderReal[50]( 0 ),
Imag[50]( 0 ),
OldImag[50]( 0 ),
OlderImag[50]( 0 ),
Ampl[50]( 0 ),
OldAmpl[50]( 0 ),
DB[50]( 0 ) ;
if CurrentBar = 1 then
begin
{ 360 / 40 = 9 }
alpha1 = ( 1 - Sine( 9 ) ) / Cosine( 9 ) ;
alpha1Plus1 = alpha1 + 1 ;
Log10 = Log( 10 ) ;
end ;
HP = 0.5 * alpha1Plus1 * ( Price - Price[1] ) +
alpha1 * HP[1] ;
SmoothHP = ( HP + 2 * HP[1] + 3 * HP[2] + 3 * HP[3] +
2 * HP[4] + HP[5] ) / 12 ;
if CurrentBar = 1 then
SmoothHP = 0
else if CurrentBar < 7 then
SmoothHP = Price - Price[1] ;
EhlersDelta = -0.015 * CurrentBar + 0.5 ;
EhlersDelta = MaxList( 0.15, EhlersDelta ) ;
if CurrentBar > 6 then
begin
for N = 8 to 50
begin
EhlersBeta = Cosine( 360 / N ) ;
Cos720Delta = Cosine( 720 * EhlersDelta / N ) ;
if Cos720Delta <> 0 then
EhlersGamma = 1 / Cos720Delta ;
alpha = EhlersGamma -
SquareRoot( Square( EhlersGamma ) - 1 ) ;
OneMinusAlpha = 1 - alpha ;
OnePlusAlpha = 1 + alpha ;
Q[N] = ( N / TwoPi ) * ( SmoothHP -
SmoothHP[1] ) ;
EhlersI[N] = SmoothHP ;
Real[N] = 0.5 * OneMinusAlpha * ( EhlersI[N] -
OlderI[N] ) + EhlersBeta * OnePlusAlpha *
OldReal[N] - alpha * OlderReal[N] ;
Imag[N] = 0.5 * OneMinusAlpha * ( Q[N] -
OlderQ[N] ) + EhlersBeta * OnePlusAlpha *
OldImag[N] - alpha * OlderImag[N] ;
Ampl[N] = ( Square( Real[N] ) +
Square( Imag[N] ) ) ;
end ;
end ;
for N = 8 to 50
begin
OlderI[N] = OldI[N] ;
OldI[N] = EhlersI[N] ;
OlderQ[N] = OldQ[N] ;
OldQ[N] = Q[N] ;
OlderReal[N] = OldReal[N] ;
OldReal[N] = Real[N] ;
OlderImag[N] = OldImag[N] ;
OldImag[N] = Imag[N] ;
OldAmpl[N] = Ampl[N] ;
end ;
MaxAmpl = Ampl[10] ;
for N = 8 to 50
begin
if Ampl[N] > MaxAmpl then
MaxAmpl = Ampl[N] ;
end ;
for N = 8 to 50
begin
if MaxAmpl <> 0 and ( Ampl[N] / MaxAmpl ) > 0 then
DB[N] = -10 * Log( 0.01 / ( 1 - .99 * Ampl[N] /
MaxAmpl ) ) / Log10 ;
if DB[N] > 20 then
DB[N] = 20 ;
end ;
Num = 0 ;
Denom = 0 ;
for N = 10 to 50
begin
if DB[N] <= 3 then
begin
Num = Num + N * ( 20 - DB[N] ) ;
Denom = Denom + ( 20 - DB[N] ) ;
end ;
if Denom <> 0 then
DC = Num / Denom ;
end ;
DomCyc = Median( DC, 10 ) ;
if ShowDC = true then
Plot1( DomCyc, "DC", RGB( 0, 0, 255 ), 0, 2 ) ;
for N = 8 to 50
begin
if DB[N] <= 10 then
begin
Color1 = 255 ;
Color2 = 255 * ( 1 - DB[N] / 10 ) ;
end ;
if DB[N] > 10 then
begin
Color1 = 255 * ( 2 - DB[N] / 10 ) ;
Color2 = 0 ;
end ;
PlotColor = RGB( Color1, Color2, 0 ) ;
if CurrentBar > 10 then
begin
switch N
begin
case 8:
Plot8( N, "S8", PlotColor, 0, 5 ) ;
case 9:
Plot9( N, "S9", PlotColor, 0, 5 ) ;
case 10:
Plot10( N, "S10", PlotColor, 0, 5 ) ;
case 11:
Plot11( N, "S11", PlotColor, 0, 5 ) ;
case 12:
Plot12( N, "S12", PlotColor, 0, 5 ) ;
case 13:
Plot13( N, "S13", PlotColor, 0, 5 ) ;
case 14:
Plot14( N, "S14", PlotColor, 0, 5 ) ;
case 15:
Plot15( N, "S15", PlotColor, 0, 5 ) ;
case 16:
Plot16( N, "S16", PlotColor, 0, 5 ) ;
case 17:
Plot17( N, "S17", PlotColor, 0, 5 ) ;
case 18:
Plot18( N, "S18", PlotColor, 0, 5 ) ;
case 19:
Plot19( N, "S19", PlotColor, 0, 5 ) ;
case 20:
Plot20( N, "S20", PlotColor, 0, 5 ) ;
case 21:
Plot21( N, "S21", PlotColor, 0, 5 ) ;
case 22:
Plot22( N, "S22", PlotColor, 0, 5 ) ;
case 23:
Plot23( N, "S23", PlotColor, 0, 5 ) ;
case 24:
Plot24( N, "S24", PlotColor, 0, 5 ) ;
case 25:
Plot25( N, "S25", PlotColor, 0, 5 ) ;
case 26:
Plot26( N, "S26", PlotColor, 0, 5 ) ;
case 27:
Plot27( N, "S27", PlotColor, 0, 5 ) ;
case 28:
Plot28( N, "S28", PlotColor, 0, 5 ) ;
case 29:
Plot29( N, "S29", PlotColor, 0, 5 ) ;
case 30:
Plot30( N, "S30", PlotColor, 0, 5 ) ;
case 31:
Plot31( N, "S31", PlotColor, 0, 5 ) ;
case 32:
Plot32( N, "S32", PlotColor, 0, 5 ) ;
case 33:
Plot33( N, "S33", PlotColor, 0, 5 ) ;
case 34:
Plot34( N, "S34", PlotColor, 0, 5 ) ;
case 35:
Plot35( N, "S35", PlotColor, 0, 5 ) ;
case 36:
Plot36( N, "S36", PlotColor, 0, 5 ) ;
case 37:
Plot37( N, "S37", PlotColor, 0, 5 ) ;
case 38:
Plot38( N, "S38", PlotColor, 0, 5 ) ;
case 39:
Plot39( N, "S39", PlotColor, 0, 5 ) ;
case 40:
Plot40( N, "S40", PlotColor, 0, 5 ) ;
case 41:
Plot41( N, "S41", PlotColor, 0, 5 ) ;
case 42:
Plot42( N, "S42", PlotColor, 0, 5 ) ;
case 43:
Plot43( N, "S43", PlotColor, 0, 5 ) ;
case 44:
Plot44( N, "S44", PlotColor, 0, 5 ) ;
case 45:
Plot45( N, "S45", PlotColor, 0, 5 ) ;
case 46:
Plot46( N, "S46", PlotColor, 0, 5 ) ;
case 47:
Plot47( N, "S47", PlotColor, 0, 5 ) ;
case 48:
Plot48( N, "S48", PlotColor, 0, 5 ) ;
case 49:
Plot49( N, "S49", PlotColor, 0, 5 ) ;
case 50:
Plot50( N, "S50", PlotColor, 0, 5 ) ;
end ;
end ;
end ;
Indicator: EhlersDominantCycle
inputs:
Price( MedianPrice ) ;
variables:
alpha1( 0 ),
alpha1Plus1( 0 ),
Log10( 0 ),
HP( 0 ),
SmoothHP( 0 ),
EhlersDelta( 0.1 ),
EhlersBeta( 0 ),
Cos720Delta( 0 ),
EhlersGamma( 0 ),
alpha( 0 ),
OneMinusAlpha( 0 ),
OnePlusAlpha( 0 ),
N( 0 ),
TwoPi( 6.2831854 ),
MaxAmpl( 0 ),
Num( 0 ),
Denom( 0 ),
DC( 0 ),
DomCyc( 0 ),
Cos720DeltaDom( 0 ),
SineLine( 0 ),
CosineLine( 0 ) ;
arrays:
EhlersI[50]( 0 ),
OldI[50]( 0 ),
OlderI[50]( 0 ),
Q[50]( 0 ),
OldQ[50]( 0 ),
OlderQ[50]( 0 ),
Real[50]( 0 ),
OldReal[50]( 0 ),
OlderReal[50]( 0 ),
Imag[50]( 0 ),
OldImag[50]( 0 ),
OlderImag[50]( 0 ),
Ampl[50]( 0 ),
OldAmpl[50]( 0 ),
DB[50]( 0 ) ;
if CurrentBar = 1 then
begin
{ 360 / 40 = 9 }
alpha1 = ( 1 - Sine( 9 ) ) / Cosine( 9 ) ;
alpha1Plus1 = alpha1 + 1 ;
Log10 = Log( 10 ) ;
end ;
HP = 0.5 * alpha1Plus1 * ( Price - Price[1] ) +
alpha1 * HP[1] ;
SmoothHP = ( HP + 2 * HP[1] + 3 * HP[2] + 3 * HP[3] +
2 * HP[4] + HP[5] ) / 12 ;
if CurrentBar = 1 then
SmoothHP = 0
else if CurrentBar < 7 then
SmoothHP = Price - Price[1] ;
EhlersDelta = -0.015 * CurrentBar + 0.5 ;
EhlersDelta = MaxList( 0.15, EhlersDelta ) ;
if CurrentBar > 6 then
begin
for N = 8 to 50
begin
EhlersBeta = Cosine( 360 / N ) ;
Cos720Delta = Cosine( 720 * EhlersDelta / N ) ;
if Cos720Delta <> 0 then
EhlersGamma = 1 / Cos720Delta ;
alpha = EhlersGamma -
SquareRoot( Square( EhlersGamma ) - 1 ) ;
OneMinusAlpha = 1 - alpha ;
OnePlusAlpha = 1 + alpha ;
Q[N] = ( N / TwoPi ) * ( SmoothHP -
SmoothHP[1] ) ;
EhlersI[N] = SmoothHP ;
Real[N] = 0.5 * OneMinusAlpha * ( EhlersI[N] -
OlderI[N] ) + EhlersBeta * OnePlusAlpha *
OldReal[N] - alpha * OlderReal[N] ;
Imag[N] = 0.5 * OneMinusAlpha * ( Q[N] -
OlderQ[N] ) + EhlersBeta * OnePlusAlpha *
OldImag[N] - alpha * OlderImag[N] ;
Ampl[N] = ( Square( Real[N] ) +
Square( Imag[N] ) ) ;
end ;
end ;
for N = 8 to 50
begin
OlderI[N] = OldI[N] ;
OldI[N] = EhlersI[N] ;
OlderQ[N] = OldQ[N] ;
OldQ[N] = Q[N] ;
OlderReal[N] = OldReal[N] ;
OldReal[N] = Real[N] ;
OlderImag[N] = OldImag[N] ;
OldImag[N] = Imag[N] ;
OldAmpl[N] = Ampl[N] ;
end ;
MaxAmpl = Ampl[10] ;
for N = 8 to 50
begin
if Ampl[N] > MaxAmpl then
MaxAmpl = Ampl[N] ;
end ;
for N = 8 to 50
begin
if MaxAmpl <> 0 and ( Ampl[N] / MaxAmpl ) > 0 then
DB[N] = -10 * Log( 0.01 / ( 1 - .99 * Ampl[N] /
MaxAmpl ) ) / Log10 ;
if DB[N] > 20 then
DB[N] = 20 ;
end ;
Num = 0 ;
Denom = 0 ;
for N = 10 to 50
begin
if DB[N] <= 3 then
begin
Num = Num + N * ( 20 - DB[N] ) ;
Denom = Denom + ( 20 - DB[N] ) ;
end ;
if Denom <> 0 then
DC = Num / Denom ;
end ;
DomCyc = Median( DC, 10 ) ;
if DomCyc < 8 then
DomCyc = 20 ;
EhlersBeta = Cosine( 360 / DomCyc ) ;
Cos720DeltaDom = Cosine( 720 * EhlersDelta / DomCyc ) ;
if Cos720DeltaDom <> 0 then
EhlersGamma = 1 / Cos720DeltaDom ;
alpha = EhlersGamma - SquareRoot( Square( EhlersGamma )
- 1 ) ;
SineLine = 0.5 * ( 1 - alpha ) * ( SmoothHP -
SmoothHP[1] ) + EhlersBeta * ( 1 + alpha ) *
SineLine[1] - alpha * SineLine[2] ;
CosineLine = ( DomCyc / TwoPi ) * ( SineLine -
SineLine[1] ) ;
if CurrentBar > 10 then
begin
Plot1( SineLine, "Sine", Red, default, 2 ) ;
Plot2( CosineLine, "Cosine", Cyan, default, 2 ) ;
end ;
Strategy: EhlerBandPassStrat
inputs:
Price( MedianPrice ) ;
variables:
alpha1( 0 ),
alpha1Plus1( 0 ),
Log10( 0 ),
HP( 0 ),
SmoothHP( 0 ),
EhlersDelta( 0.1 ),
EhlersBeta( 0 ),
Cos720Delta( 0 ),
EhlersGamma( 0 ),
alpha( 0 ),
OneMinusAlpha( 0 ),
OnePlusAlpha( 0 ),
N( 0 ),
TwoPi( 6.2831854 ),
MaxAmpl( 0 ),
Num( 0 ),
Denom( 0 ),
DC( 0 ),
DomCyc( 0 ),
Cos720DeltaDom( 0 ),
SineLine( 0 ),
CosineLine( 0 ) ;
arrays:
EhlersI[50]( 0 ),
OldI[50]( 0 ),
OlderI[50]( 0 ),
Q[50]( 0 ),
OldQ[50]( 0 ),
OlderQ[50]( 0 ),
Real[50]( 0 ),
OldReal[50]( 0 ),
OlderReal[50]( 0 ),
Imag[50]( 0 ),
OldImag[50]( 0 ),
OlderImag[50]( 0 ),
Ampl[50]( 0 ),
OldAmpl[50]( 0 ),
DB[50]( 0 ) ;
if CurrentBar = 1 then
begin
{ 360 / 40 = 9 }
alpha1 = ( 1 - Sine( 9 ) ) / Cosine( 9 ) ;
alpha1Plus1 = alpha1 + 1 ;
Log10 = Log( 10 ) ;
end ;
HP = 0.5 * alpha1Plus1 * ( Price - Price[1] ) +
alpha1 * HP[1] ;
SmoothHP = ( HP + 2 * HP[1] + 3 * HP[2] + 3 * HP[3] +
2 * HP[4] + HP[5] ) / 12 ;
if CurrentBar = 1 then
SmoothHP = 0
else if CurrentBar < 7 then
SmoothHP = Price - Price[1] ;
EhlersDelta = -0.015 * CurrentBar + 0.5 ;
EhlersDelta = MaxList( 0.15, EhlersDelta ) ;
if CurrentBar > 6 then
begin
for N = 8 to 50
begin
EhlersBeta = Cosine( 360 / N ) ;
Cos720Delta = Cosine( 720 * EhlersDelta / N ) ;
if Cos720Delta <> 0 then
EhlersGamma = 1 / Cos720Delta ;
alpha = EhlersGamma -
SquareRoot( Square( EhlersGamma ) - 1 ) ;
OneMinusAlpha = 1 - alpha ;
OnePlusAlpha = 1 + alpha ;
Q[N] = ( N / TwoPi ) * ( SmoothHP -
SmoothHP[1] ) ;
EhlersI[N] = SmoothHP ;
Real[N] = 0.5 * OneMinusAlpha * ( EhlersI[N] -
OlderI[N] ) + EhlersBeta * OnePlusAlpha *
OldReal[N] - alpha * OlderReal[N] ;
Imag[N] = 0.5 * OneMinusAlpha * ( Q[N] -
OlderQ[N] ) + EhlersBeta * OnePlusAlpha *
OldImag[N] - alpha * OlderImag[N] ;
Ampl[N] = ( Square( Real[N] ) +
Square( Imag[N] ) ) ;
end ;
end ;
for N = 8 to 50
begin
OlderI[N] = OldI[N] ;
OldI[N] = EhlersI[N] ;
OlderQ[N] = OldQ[N] ;
OldQ[N] = Q[N] ;
OlderReal[N] = OldReal[N] ;
OldReal[N] = Real[N] ;
OlderImag[N] = OldImag[N] ;
OldImag[N] = Imag[N] ;
OldAmpl[N] = Ampl[N] ;
end ;
MaxAmpl = Ampl[10] ;
for N = 8 to 50
begin
if Ampl[N] > MaxAmpl then
MaxAmpl = Ampl[N] ;
end ;
for N = 8 to 50
begin
if MaxAmpl <> 0 and ( Ampl[N] / MaxAmpl ) > 0 then
DB[N] = -10 * Log( 0.01 / ( 1 - .99 * Ampl[N] /
MaxAmpl ) ) / Log10 ;
if DB[N] > 20 then
DB[N] = 20 ;
end ;
Num = 0 ;
Denom = 0 ;
for N = 10 to 50
begin
if DB[N] <= 3 then
begin
Num = Num + N * ( 20 - DB[N] ) ;
Denom = Denom + ( 20 - DB[N] ) ;
end ;
if Denom <> 0 then
DC = Num / Denom ;
end ;
DomCyc = Median( DC, 10 ) ;
if DomCyc < 8 then
DomCyc = 20 ;
EhlersBeta = Cosine( 360 / DomCyc ) ;
Cos720DeltaDom = Cosine( 720 * EhlersDelta / DomCyc ) ;
if Cos720DeltaDom <> 0 then
EhlersGamma = 1 / Cos720DeltaDom ;
alpha = EhlersGamma - SquareRoot( Square( EhlersGamma )
- 1 ) ;
SineLine = 0.5 * ( 1 - alpha ) * ( SmoothHP -
IndicatorIndicator SmoothHP[1] ) + EhlersBeta * ( 1 + alpha ) *
SineLine[1] - alpha * SineLine[2] ;
CosineLine = ( DomCyc / TwoPi ) * ( SineLine -
SineLine[1] ) ;
if CurrentBar > 10 then
begin
if CosineLine crosses over SineLine then
Buy next bar market
else if CosineLine crosses under SineLine then
Sell short next bar at market ;
end ;
--Mark Mills
TradeStation Securities, Inc.
A subsidiary of TradeStation Group, Inc.
www.TradeStation.com
GO BACK
eSIGNAL: MEASURING CYCLE PERIODS
For this month's tip, we've provided the eSignal formulas named "ChRSpectrum.efs"
and "DCTunedBypassFilter.efs" based on the code given in John Ehlers' article
in this issue, "Measuring Cycle Periods."
Both studies contain formula parameters that may be configured through
the Edit Studies option in the Advanced Chart to change the color and thickness
of the indicators. The spectrum study also has a parameter to turn on/off
the dominant cycle display. A sample chart is shown in Figure 2.
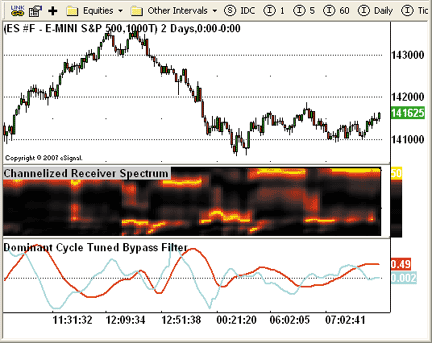
FIGURE 2: eSIGNAL, EHLERS CYCLE INDICATORS. Here is
a demonstration of Ehlers' spectrum indicator and dominant cycle tuned
bypass filter in eSignal.
To discuss these studies or download complete copies of the formulas,
please visit the EFS Library Discussion Board forum under the Forums link
at www.esignalcentral.com or visit our EFS KnowledgeBase at www.esignalcentral.com/support/kb/efs/.
ChRSpectrum.efs:
/***************************************
Provided By : eSignal (c) Copyright 2008
Description: Measuring Cycle Periods
by John Ehlers
Version 1.0 1/04/2008
Notes:
* March 2008 Issue of Stocks and Commodities Magazine
* Study requires version 8.0 or later.
Formula Parameters: Default:
Show Dominant Cycle false
Dominant Cycle Color blue
Dominant Cycle Size 2
*****************************************************************/
function preMain() {
setStudyTitle("Channelized Receiver Spectrum ");
setShowCursorLabel(false);
setShowTitleParameters(false);
// Dominant Cycle properties
setPlotType(PLOTTYPE_CIRCLE, 51);
setDefaultBarBgColor(Color.black, 0);
var fp1 = new FunctionParameter("bShowDC", FunctionParameter.BOOLEAN);
fp1.setName("Show Dominant Cycle");
fp1.setDefault(false);
var fp2 = new FunctionParameter("nDC_color", FunctionParameter.COLOR);
fp2.setName("Dominant Cycle Color");
fp2.setDefault(Color.blue);
var fp3 = new FunctionParameter("nDC_thick", FunctionParameter.NUMBER);
fp3.setName("Dominant Cycle Size");
fp3.setLowerLimit(1);
fp3.setDefault(2);
}
// Global Variables
var bVersion = null; // Version flag
var bInit = false; // Initialization flag
var xPrice = null;
var xHP = null;
var xCleanData = null;
var aDB = new Array(51);
var aReturn = new Array(52); // return array
var nDelta = 0.1;
var nBeta = 0;
var nGamma = 0;
var nAlpha = 0;
var nMaxAmpl = 0;
var nNum = 0;
var nDenom = 0;
var nDC = 0;
var nDomCyc = 0;
var aDC = new Array(10);
var aQ = new Array(51);
var aI = new Array(51);
var aReal = new Array(51);
var aOlderI = new Array(51);
var aOldReal = new Array(51);
var aOlderReal = new Array(51);
var aImag = new Array(51);
var aOldQ = new Array(51);
var aOlderQ = new Array(51);
var aOldImag = new Array(51);
var aOlderImag = new Array(51);
var aAmpl = new Array(51);
var aOldI = new Array(51);
var aOldAmpl = new Array(51);
for (var j = 0; j < 51; j++) {
aQ[j] = 0;
aI[j] = 0;
aReal[j] = 0;
aOlderI[j] = 0;
aOldReal[j] = 0;
aOlderReal[j] = 0;
aImag[j] = 0;
aOldQ[j] = 0;
aOlderQ[j] = 0;
aOldImag[j] = 0;
aOlderImag[j] = 0;
aAmpl[j] = 0;
aOldI[j] = 0;
aOldAmpl[j] = 0;
}
function main(bShowDC, nDC_color, nDC_thick) {
if (bVersion == null) bVersion = verify();
if (bVersion == false) return;
var nPeriod = 0;
var n = 0;
var nMaxPwr = 0;
var nNum = 0;
var nDenom = 0;
var nDominantCycle = 0;
var Color1 = null;
var Color2 = null;
var nState = getBarState();
//Initialization
if (bInit == false) {
drawTextPixel(0, 0, " ", null,
Color.lightgrey, Text.RELATIVETOTOP|Text.RELATIVETOLEFT, null, 12, "bkg");
setDefaultBarFgColor(nDC_color, 51);
setDefaultBarThickness(nDC_thick, 51);
xPrice = hl2();
xHP = efsInternal("calcHP", xPrice);
xCleanData = efsInternal("calcCleanData", xHP, xPrice); // Smooth HP
bInit = true;
}
if (nState == BARSTATE_NEWBAR) {
aDC.pop();
aDC.unshift(nDC);
}
if (nState == BARSTATE_NEWBAR) {
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
aOlderI[nPeriod] = aOldI[nPeriod];
aOldI[nPeriod] = aI[nPeriod];
aOlderQ[nPeriod] = aOldQ[nPeriod];
aOldQ[nPeriod] = aQ[nPeriod];
aOlderReal[nPeriod] = aOldReal[nPeriod];
aOldReal[nPeriod] = aReal[nPeriod];
aOlderImag[nPeriod] = aOldImag[nPeriod];
aOldImag[nPeriod] = aImag[nPeriod];
aOldAmpl[nPeriod] = aAmpl[nPeriod];
}
}
var nHP = xHP.getValue(0);
var nCleanData = xCleanData.getValue(-50);
if (nHP == null || nCleanData == null) return;
nDelta = -.015 * getCurrentBarCount() + .5;
if (nDelta < .15 ) {
nDelta = .15;
}
if (getCurrentBarCount() > 6 ) {
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
nBeta = Math.cos((2*Math.PI)/nPeriod);
nGamma = 1 / Math.cos((((2*Math.PI)+(2*Math.PI)) * nDelta) / nPeriod);
nAlpha = nGamma - Math.sqrt(nGamma*nGamma - 1);
aQ[nPeriod] = (nPeriod / 6.283185)*(xCleanData.getValue(0) - xCleanData.getValue(-1));
aI[nPeriod] = xCleanData.getValue(0);
aReal[nPeriod] = .5*(1 - nAlpha)*(aI[nPeriod] - aOlderI[nPeriod])
+ nBeta*(1 + nAlpha)*aOldReal[nPeriod] - nAlpha*aOlderReal[nPeriod];
aImag[nPeriod] = .5*(1 - nAlpha)*(aQ[nPeriod] - aOlderQ[nPeriod])
+ nBeta*(1 + nAlpha)*aOldImag[nPeriod] - nAlpha*aOlderImag[nPeriod];
aAmpl[nPeriod] = (aReal[nPeriod]*aReal[nPeriod] + aImag[nPeriod]*aImag[nPeriod]);
}
}
nMaxAmpl = aAmpl[10];
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (aAmpl[nPeriod] > nMaxAmpl) {
nMaxAmpl = aAmpl[nPeriod];
}
}
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (nMaxAmpl != 0 && (aAmpl[nPeriod] / nMaxAmpl) > 0 ) {
aDB[nPeriod] = -10 * Math.log(.01 / (1 - .99*aAmpl[nPeriod] / nMaxAmpl)) / Math.log(10);
}
if (aDB[nPeriod] > 20 ) {
aDB[nPeriod] = 20;
}
}
nNum = 0;
nDemon = 0;
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (aDB[nPeriod] <= 3 ) {
nNum = nNum + nPeriod*(20 - aDB[nPeriod]);
nDenom = nDenom + (20 - aDB[nPeriod]);
}
if (nDenom != 0 ) {
nDC = nNum / nDenom;
aDC[0] = nDC;
}
}
nDomCyc = Median(aDC, 10);
if (bShowDC == true) {
aReturn[51] = nDomCyc;
}
//Plot the Spectrum as a Heatmap
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (aDB[nPeriod] <= 10) {
Color1 = 255;
Color2 = Math.round(255*(1 - aDB[nPeriod]/10));
}
if (aDB[nPeriod] > 10) {
Color1 = Math.round(255*(2 - aDB[nPeriod]/10));
Color2 = 0;
}
aReturn[nPeriod] = nPeriod;
setDefaultBarFgColor(Color.RGB(Color1 , Color2, 0), nPeriod);
setDefaultBarThickness(4, nPeriod);
}
// aReturn[51] // contains the Dominant Cycle value
return aReturn;
}
// calcHP globals
var nPrevHP = null;
var nCurrHP = null;
function calcHP(x) {
var nAlpha1 = (1 - Math.sin((2*Math.PI)/40)) / Math.cos((2*Math.PI)/40);
var nHP = null;
if (getCurrentBarCount() <= 5 ) {
nCurrHP = x.getValue(0);
return nCurrHP;
} else {
if (x.getValue(-1) == null) return null;
if (getBarState() == BARSTATE_NEWBAR) nPrevHP = nCurrHP;
nCurrHP = ( 0.5*(1 + nAlpha1)*(x.getValue(0) - x.getValue(-1)) + nAlpha1*nPrevHP );
return nCurrHP;
}
}
function calcCleanData(x, xP) { //SmoothHP
if (getCurrentBarCount() == 1 ) {
return 0;
} else if (getCurrentBarCount() <= 7 ) {
return xP.getValue(0) - xP.getValue(-1);
} else {
return ( x.getValue(0) +
2*x.getValue(-1) +
3*x.getValue(-2) +
3*x.getValue(-3) +
2*x.getValue(-4) +
x.getValue(-5) ) / 12;
}
}
function Median(myArray, Length) {
var aArray = new Array(Length);
var nMedian = null;
for (var i = 0; i < Length; i++) {
aArray[i] = myArray[i];
}
aArray = aArray.sort(compareNumbers);
nMedian = aArray[Math.round((Length-1)/2)];
return nMedian;
}
function compareNumbers(a, b) {
return a - b
}
function verify() {
var b = false;
if (getBuildNumber() < 779) {
drawTextAbsolute(5, 35, "This study requires version 8.0 or later.",
Color.white, Color.blue, Text.RELATIVETOBOTTOM|Text.RELATIVETOLEFT|Text.BOLD|Text.LEFT,
null, 13, "error");
drawTextAbsolute(5, 20, "Click HERE to upgrade.@URL=https://www.esignal.com/download/default.asp",
Color.white, Color.blue, Text.RELATIVETOBOTTOM|Text.RELATIVETOLEFT|Text.BOLD|Text.LEFT,
null, 13, "upgrade");
return b;
} else {
b = true;
}
return b;
}
______________________________________________________________________
DCTunedBypassFilter.efs:
/***************************************
Provided By : eSignal (c) Copyright 2008
Description: Measuring Cycle Periods
by John Ehlers
Version 1.0 1/04/2008
Notes:
* March 2008 Issue of Stocks and Commodities Magazine
* Study requires version 8.0 or later.
Formula Parameters: Default:
Sine Color red
Cosine Color cyan
Sine Thickness 2
Cosine Thickness 2
*****************************************************************/
function preMain() {
setStudyTitle("Dominant Cycle Tuned Bypass Filter ");
setShowTitleParameters(false);
setCursorLabelName("Sine", 0);
setCursorLabelName("Cosine", 1);
var fp1 = new FunctionParameter("nS_color", FunctionParameter.COLOR);
fp1.setName("Sine Color");
fp1.setDefault(Color.red);
var fp2 = new FunctionParameter("nC_color", FunctionParameter.COLOR);
fp2.setName("Cosine Color");
fp2.setDefault(Color.cyan);
var fp3 = new FunctionParameter("nS_thick", FunctionParameter.NUMBER);
fp3.setName("Sine Thickness");
fp3.setLowerLimit(1);
fp3.setDefault(2);
var fp4 = new FunctionParameter("nC_thick", FunctionParameter.NUMBER);
fp4.setName("Cosine Thickness");
fp4.setLowerLimit(1);
fp4.setDefault(2);
}
// Global Variables
var bVersion = null; // Version flag
var bInit = false; // Initialization flag
var xPrice = null;
var xHP = null;
var xCleanData = null;
var aDB = new Array(51);
var nDelta = 0.1;
var nBeta = 0;
var nGamma = 0;
var nAlpha = 0;
var nMaxAmpl = 0;
var nNum = 0;
var nDenom = 0;
var nDC = 0;
var nDomCyc = 0;
var nValue1 = null;
var nValue1_1 = null;
var nValue1_2 = null;
var nValue2 = null;
var aDC = new Array(10);
var aQ = new Array(51);
var aI = new Array(51);
var aReal = new Array(51);
var aOlderI = new Array(51);
var aOldReal = new Array(51);
var aOlderReal = new Array(51);
var aImag = new Array(51);
var aOldQ = new Array(51);
var aOlderQ = new Array(51);
var aOldImag = new Array(51);
var aOlderImag = new Array(51);
var aAmpl = new Array(51);
var aOldI = new Array(51);
var aOldAmpl = new Array(51);
for (var j = 0; j < 51; j++) {
aQ[j] = 0;
aI[j] = 0;
aReal[j] = 0;
aOlderI[j] = 0;
aOldReal[j] = 0;
aOlderReal[j] = 0;
aImag[j] = 0;
aOldQ[j] = 0;
aOlderQ[j] = 0;
aOldImag[j] = 0;
aOlderImag[j] = 0;
aAmpl[j] = 0;
aOldI[j] = 0;
aOldAmpl[j] = 0;
}
function main(nS_color, nC_color, nS_thick, nC_thick) {
if (bVersion == null) bVersion = verify();
if (bVersion == false) return;
var nPeriod = 0;
var n = 0;
var nMaxPwr = 0;
var nNum = 0;
var nDenom = 0;
var nDominantCycle = 0;
var Color1 = null;
var Color2 = null;
var nState = getBarState();
//Initialization
if (bInit == false) {
setDefaultBarFgColor(nS_color, 0);
setDefaultBarFgColor(nC_color, 1);
setDefaultBarThickness(nS_thick, 0);
setDefaultBarThickness(nC_thick, 1);
xPrice = hl2();
xHP = efsInternal("calcHP", xPrice);
xCleanData = efsInternal("calcCleanData", xHP, xPrice); // Smooth HP
bInit = true;
}
if (nState == BARSTATE_NEWBAR) {
aDC.pop();
aDC.unshift(nDC);
nValue1_2 = nValue1_1;
nValue1_1 = nValue1;
}
if (nState == BARSTATE_NEWBAR) {
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
aOlderI[nPeriod] = aOldI[nPeriod];
aOldI[nPeriod] = aI[nPeriod];
aOlderQ[nPeriod] = aOldQ[nPeriod];
aOldQ[nPeriod] = aQ[nPeriod];
aOlderReal[nPeriod] = aOldReal[nPeriod];
aOldReal[nPeriod] = aReal[nPeriod];
aOlderImag[nPeriod] = aOldImag[nPeriod];
aOldImag[nPeriod] = aImag[nPeriod];
aOldAmpl[nPeriod] = aAmpl[nPeriod];
}
}
var nHP = xHP.getValue(0);
var nCleanData = xCleanData.getValue(-50);
if (nHP == null || nCleanData == null) return;
nDelta = -.015 * getCurrentBarCount() + .5;
if (nDelta < .15 ) {
nDelta = .15;
}
if (getCurrentBarCount() > 6 ) {
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
nBeta = Math.cos((2*Math.PI)/nPeriod);
nGamma = 1 / Math.cos((((2*Math.PI)+(2*Math.PI)) * nDelta) / nPeriod);
nAlpha = nGamma - Math.sqrt(nGamma*nGamma - 1);
aQ[nPeriod] = (nPeriod / 6.283185)*(xCleanData.getValue(0) - xCleanData.getValue(-1));
aI[nPeriod] = xCleanData.getValue(0);
aReal[nPeriod] = .5*(1 - nAlpha)*(aI[nPeriod] - aOlderI[nPeriod])
+ nBeta*(1 + nAlpha)*aOldReal[nPeriod] - nAlpha*aOlderReal[nPeriod];
aImag[nPeriod] = .5*(1 - nAlpha)*(aQ[nPeriod] - aOlderQ[nPeriod])
+ nBeta*(1 + nAlpha)*aOldImag[nPeriod] - nAlpha*aOlderImag[nPeriod];
aAmpl[nPeriod] = (aReal[nPeriod]*aReal[nPeriod] + aImag[nPeriod]*aImag[nPeriod]);
}
}
nMaxAmpl = aAmpl[10];
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (aAmpl[nPeriod] > nMaxAmpl) {
nMaxAmpl = aAmpl[nPeriod];
}
}
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (nMaxAmpl != 0 && (aAmpl[nPeriod] / nMaxAmpl) > 0 ) {
aDB[nPeriod] = -10 * Math.log(.01 / (1 - .99*aAmpl[nPeriod] / nMaxAmpl)) / Math.log(10);
}
if (aDB[nPeriod] > 20 ) {
aDB[nPeriod] = 20;
}
}
nNum = 0;
nDemon = 0;
nPeriod = 8;
for (nPeriod = 8; nPeriod <= 50; nPeriod++) {
if (aDB[nPeriod] <= 3 ) {
nNum = nNum + nPeriod*(20 - aDB[nPeriod]);
nDenom = nDenom + (20 - aDB[nPeriod]);
}
if (nDenom != 0 ) {
nDC = nNum / nDenom;
aDC[0] = nDC;
}
}
nDomCyc = Median(aDC, 10);
if (nDomCyc < 8 ) {
nDomCyc = 20;
}
nBeta = Math.cos((2*Math.PI)/nDomCyc);
nGamma = 1 / Math.cos((((2*Math.PI)+(2*Math.PI)) * nDelta) / nDomCyc);
nAlpha = nGamma - Math.sqrt(nGamma*nGamma - 1);
nValue1 = .5*(1 - nAlpha)*(xCleanData.getValue(0) - xCleanData.getValue(-1)) +
nBeta*(1 + nAlpha)*nValue1_1 - nAlpha*nValue1_2;
nValue2 = (nDomCyc / 6.28)*(nValue1 - nValue1_1);
return new Array(nValue1, nValue2);
}
// calcHP globals
var nPrevHP = null;
var nCurrHP = null;
function calcHP(x) {
var nAlpha1 = (1 - Math.sin((2*Math.PI)/40)) / Math.cos((2*Math.PI)/40);
var nHP = null;
if (getCurrentBarCount() <= 5 ) {
nCurrHP = x.getValue(0);
return nCurrHP;
} else {
if (x.getValue(-1) == null) return null;
if (getBarState() == BARSTATE_NEWBAR) nPrevHP = nCurrHP;
nCurrHP = ( 0.5*(1 + nAlpha1)*(x.getValue(0) - x.getValue(-1)) + nAlpha1*nPrevHP );
return nCurrHP;
}
}
function calcCleanData(x, xP) { //SmoothHP
if (getCurrentBarCount() == 1 ) {
return 0;
} else if (getCurrentBarCount() <= 7 ) {
return xP.getValue(0) - xP.getValue(-1);
} else {
return ( x.getValue(0) +
2*x.getValue(-1) +
3*x.getValue(-2) +
3*x.getValue(-3) +
2*x.getValue(-4) +
x.getValue(-5) ) / 12;
}
}
function Median(myArray, Length) {
var aArray = new Array(Length);
var nMedian = null;
for (var i = 0; i < Length; i++) {
aArray[i] = myArray[i];
}
aArray = aArray.sort(compareNumbers);
nMedian = aArray[Math.round((Length-1)/2)];
return nMedian;
}
function compareNumbers(a, b) {
return a - b
}
function verify() {
var b = false;
if (getBuildNumber() < 779) {
drawTextAbsolute(5, 35, "This study requires version 8.0 or later.",
Color.white, Color.blue, Text.RELATIVETOBOTTOM|Text.RELATIVETOLEFT|Text.BOLD|Text.LEFT,
null, 13, "error");
drawTextAbsolute(5, 20, "Click HERE to upgrade.@URL=https://www.esignal.com/download/default.asp",
Color.white, Color.blue, Text.RELATIVETOBOTTOM|Text.RELATIVETOLEFT|Text.BOLD|Text.LEFT,
null, 13, "upgrade");
return b;
} else {
b = true;
}
return b;
}
--Jason Keck
eSignal, a division of Interactive Data Corp.
800 815-8256, www.esignalcentral.com
GO BACK
WEALTH-LAB: MEASURING CYCLE PERIODS
We've coded John Ehlers' filter bank to measure the dominant cycle
(DC) and the sine and cosine filter components in WealthScript for Wealth-Lab
version 5.0 (.Net), based on John Ehlers' article in this issue, "Measuring
Cycle Periods."
The CycleFilterDC function plots and returns the DC series and its components,
so it's a trivial matter to make use of them in a trading strategy.
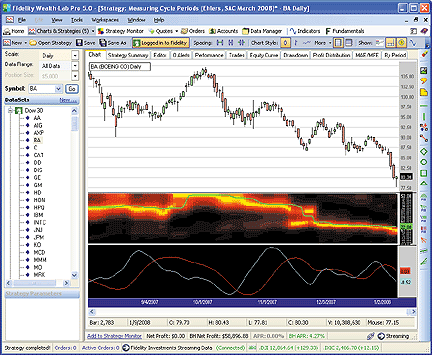
FIGURE 3: WEALTH-LAB, DOMINANT CYCLE. In this daily
chart of cyclical price action, you can just about verify the dominant
cycle measurement (plotted in lime green on the heat map) by visual inspection.
WealthScript code:
/* Code for the WealthLab.Strategies namespace */
public class MeasuringCyclePeriods : WealthScript
{
public class ArrayHolder
{ // current, old, older
internal double I, I2, I3;
internal double Q, Q2, Q3;
internal double R, R2, R3;
internal double Im, Im2, Im3;
internal double A;
internal double dB;
}
public DataSeries CycleFilterDC(DataSeries ds, out DataSeries sine, out DataSeries cosine)
{
double twoPi = 2 * Math.PI;
// Initialize arrays
ArrayHolder[] ah = new ArrayHolder[51];
for( int n = 8; n < 51; n++ )
ah[n] = new ArrayHolder();
Color[] color = new Color[21];
DataSeries[] DB = new DataSeries[51];
double domCycle = 0d;
string name = ds.Description;
DataSeries result = Close - Close;
result.Description = "Dominant Cycle(" + name + ")";
// Create and plot the decibel series - change the colors later
ChartPane dbPane = CreatePane(40, false, false );
for( int n = 8; n < 51; n++ ) {
DB[n] = result + n;
DB[n].Description = "Cycle." + n.ToString();
PlotSeries(dbPane, DB[n], Color.Black, LineStyle.Solid, 6);
}
// Convert decibels to RGB color for display
for( int n = 0; n <= 10; n++ ) // yellow to red: 0 to 10 dB
color[n] = Color.FromArgb(255, (int)(255 - (255 * n / 10)), 0);
for( int n = 11; n <= 20; n++ ) // red to black: 11 to 20 db
color[n] = Color.FromArgb( (int)(255 * (20 - n)/10 ), 0, 0);
// Detrend data by High Pass Filtering with a 40 Period cutoff
DataSeries HP = result;
double alpha = (1 - Math.Sin(twoPi/40)) / Math.Cos(twoPi/40);
for(int bar = 1; bar < Bars.Count; bar++)
HP[bar] = 0.5 * (1 + alpha)* Momentum.Series(ds, 1)[bar] + alpha * HP[bar-1];
DataSeries smoothHP = FIR.Series(HP, "1,2,3,3,2,1");
for( int bar = 6; bar < Bars.Count; bar++ )
{
double maxAmpl = 0;
double delta = -0.015 * bar + 0.5;
delta = delta < 0.15 ? 0.15 : delta;
for( int n = 8; n < 51; n++ )
{
double beta = Math.Cos(twoPi / n);
double g = 1 / Math.Cos(2 * twoPi * delta / n);
double a = g - Math.Sqrt(g * g - 1);
ah[n].Q = Momentum.Series(smoothHP, 1)[bar] * n / twoPi;
ah[n].I = smoothHP[bar];
ah[n].R = 0.5 * (1 - a) * (ah[n].I - ah[n].I3) + beta * (1 + a) * ah[n].R2 - a * ah[n].R3;
ah[n].Im = 0.5 * (1 - a) * (ah[n].Q - ah[n].Q3) + beta * (1 + a) * ah[n].Im2 - a * ah[n].Im3;
ah[n].A = ah[n].R * ah[n].R + ah[n].Im * ah[n].Im;
maxAmpl = ah[n].A > maxAmpl ? ah[n].A : maxAmpl;
}
double num = 0; double den = 0;
for( int n = 8; n < 51; n++ )
{
if( maxAmpl != 0 && ah[n].A / maxAmpl > 0 )
ah[n].dB = 10 * Math.Log10( (1 - 0.99 * ah[n].A / maxAmpl) / 0.01 );
ah[n].dB = ah[n].dB > 20 ? 20 : ah[n].dB;
SetSeriesBarColor(bar, DB[n], color[(int)Math.Round(ah[n].dB)]);
if( ah[n].dB <= 3 ) {
num = num + n * (20 - ah[n].dB);
den = den + (20 - ah[n].dB);
}
if( den > 0 ) domCycle = num/den;
result[bar] = domCycle;
ah[n].I3 = ah[n].I2;
ah[n].I2 = ah[n].I;
ah[n].Q3 = ah[n].Q2;
ah[n].Q2 = ah[n].Q;
ah[n].R3 = ah[n].R2;
ah[n].R2 = ah[n].R;
ah[n].Im3 = ah[n].Im2;
ah[n].Im2 = ah[n].Im;
}
}
result = Median.Series(result, 10);
PlotSeries(dbPane, result, Color.Lime, WealthLab.LineStyle.Solid, 2);
// sine and cosine components
sine = Low - Low; sine.Description = "sine(DC)";
double a2 = 0d;
for(int bar = 10; bar < Bars.Count; bar++)
{
double delta = -0.015 * bar + 0.5;
delta = delta < 0.15 ? 0.15 : delta;
double beta = Math.Cos(2 * Math.PI / result[bar] );
double g = 1 / Math.Cos(4 * Math.PI * delta / result[bar]);
if( g < 1 )
a2 = 0;
else
a2 = g - Math.Sqrt(g * g - 1);
sine[bar] = 0.5 * (1 - a2) * Momentum.Value(bar, smoothHP, 1)
+ beta * (1 + a2) * sine[bar-1] - a2 * sine[bar-2];
}
cosine = ( result / 6.28 ) * ( sine - (sine >> 1) );
cosine.Description = "cosine(DC)";
ChartPane sinePane = CreatePane( 40, false, false );
for(int bar = 0; bar < Bars.Count; bar++)
SetPaneBackgroundColor(sinePane, bar, Color.Black);
PlotSeries(sinePane, sine, Color.Red, LineStyle.Solid, 1);
PlotSeries(sinePane, cosine, Color.Cyan, LineStyle.Solid, 1);
return result;
}
protected override void Execute()
{
HideVolume();
DataSeries avgPrice = (High + Low) / 2;
avgPrice.Description = "Avg Price";
// Get the dominant cycle, sine and cosine, and plot the heat map
DataSeries sine, cosine;
DataSeries DC = CycleFilterDC(avgPrice, out sine, out cosine);
/* Use the DC, sine, and cosine DataSeries in a Trading Strategy here */
}
--Robert Sucher
www.wealth-lab.com
GO BACK
AMIBROKER: MEASURING CYCLE PERIODS
In "Measuring Cycle Periods" in this issue, author John Ehlers presents
a very interesting technique of measuring dominant market cycle periods
by means of multiple bandpass filtering. By utilizing an approach similar
to audio equalizers, the signal (here, the price series) is fed into a
set of simple second-order infinite impulse response bandpass filters.
Filters are tuned to 8,9,10,...,50 periods. The filter with the highest
output represents the dominant cycle. Implementing the idea presented in
the article is easy using the AmiBroker Formula Language.
Listing 1 shows a full-featured formula that implements a high-pass
filter and a six-tap low-pass Fir filter on input, then 42 parallel Iir
band-pass filters. Finally, it plots the spectrogram as a heat map. A sample
chart is shown in Figure 4.
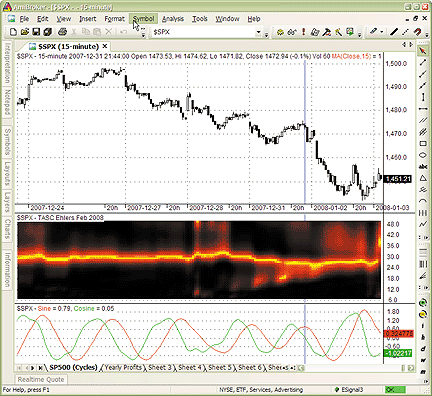
FIGURE 4: AMIBROKER, EHLERS' DOMINANT CYCLE INDICATORS.
Here
is a sample 15-minute S&P 500 index price chart with a channelized
receiver spectrum display (middle pane) and dominant cycle-tuned band-pass
filter response (bottom pane).
As an option, the formula can also plot a dominant cycle-tuned band-pass
filter response. To do so, the user needs to open the Parameters dialog
and turn on "tuned filter display."
LISTING 1: Spectrum derived from filter bank and dominant cycle-tuned filter
PI = 3.1415926;
Data = (H+L)/2;
// detrending ( high-pass filter )
HFPeriods = Param("HP filter cutoff", 40, 20, 100 );
alpha1 = ( 1-sin(2*pi/HFPeriods) ) / cos( 2 * pi / HFPeriods );
HP = AMA2( Data - Ref( Data, -1 ), 0.5 * ( 1 + alpha1 ), alpha1 );
// 6-tap low-pass FIR filter
SmoothHP = ( HP + 2 * Ref( HP, -1 ) + 3 * Ref( HP, -2 ) +
3 * Ref( HP, -3 ) + 2 * Ref( HP, -4 ) + Ref( HP, -5 ) )/12;
SmoothHPDiff = SmoothHP - Ref( SmoothHP, -1 );
x = BarIndex();
delta = -0.015 * x + 0.5;
delta = Max( delta, 0.15 );
Q = 0;
Real = 0;
Imag = 0;
Ampl = 0;
DB = 0;
I = SmoothHP;
MaxAmpl = 0;
for( N = 8; N <= 50; N++ )
{
beta = cos( 2 * PI / N );
Q = ( N / ( 2 * PI ) ) * SmoothHPDiff;
for( bar = 8; bar < BarCount; bar++ )
{
gamma = 1 / cos( 4 * PI * delta[ bar ] / N );
alpha = gamma - sqrt( gamma ^ 2 - 1 );
Real[ bar ] = 0.5 * ( 1 - alpha ) * ( I[ bar ] - I[ bar - 1 ] ) +
beta * ( 1 + alpha ) * Real[ bar - 1 ] -
alpha * Real[ bar - 2 ];
Imag[ bar ] = 0.5 * ( 1- alpha ) * ( Q[ bar ] - Q[ bar - 1 ] ) +
beta * ( 1 + alpha ) * Imag[ bar - 1 ] -
alpha * Imag[ bar - 2 ];
}
Ampl = Real ^ 2 + Imag ^ 2;
MaxAmpl = Max( MaxAmpl, Ampl );
VarSet("Ampl"+N, Ampl );
}
TunedFilterDisplay = ParamToggle("Dom Cycle Tuned Filter", "No|Yes" );
// Plot Heat Map ( Spectrogram )
// and find dominant cycle
DcNum = DcDenom = 0;
for( N = 8; N <= 50; N++ )
{
Ampl = VarGet("Ampl"+N);
db = Nz( -10 * log10( 0.01 / ( 1 - 0.99 * Ampl / MaxAmpl ) ) );
db = Min( db, 20 ) ;
Red = IIf( db <= 10, 255, 255 * ( 2 - db/10 ) );
Green = IIf( db <= 10, 255 * ( 1 - db/10 ), 0 );
if( NOT TunedFilterDisplay )
PlotOHLC( N, N, N-1, N-1, "", ColorRGB( Red, Green, 0 ),
styleCloud | styleNoLabel );
DcNum = DcNum + (db < 3 ) * N * ( 20 - db );
DcDenom = DcDenom + ( db < 3 ) * ( 20 - db );
}
DC = DcNum / DcDenom;
if( ParamToggle("Show Dom. Cycle?", "No|Yes" ) )
{
DomCycle = Median( DC, 10 );
Plot( DomCycle, "Dominant Cycle", colorBlue );
}
if( TunedFilterDisplay )
{
DomCycle = Median( DC, 10 );
DomCycle = Max( DomCycle, 8 );
Value = 0;
for( bar = 10; bar < BarCount; bar++ )
{
beta = cos( 2 * PI / domCycle[ bar ] );
gamma = 1 / cos( 4 * PI * delta[ bar ] / DomCycle[ bar ] );
alpha = gamma - sqrt( gamma ^ 2 - 1 );
Value[ bar ] = 0.5 * ( 1 - alpha ) * SmoothHPDiff[ bar ] +
beta * ( 1 + alpha ) * Value[ bar - 1 ] -
alpha * Value[ bar - 2 ];
}
Value2 = ( domCycle / ( 2 * PI ) ) * ( Value - Ref( Value, -1 ) );
Plot( Value, "Sine", colorRed );
Plot( Value2, "Cosine", colorGreen );
}
GraphZOrder = 1;
--Tomasz Janeczko, AmiBroker.com
www.amibroker.com
GO BACK
NEUROSHELL TRADER: MEASURING CYCLE PERIODS
John Ehlers' bandpass dominant cycle and dominant cycle-tuned bandpass
filter response indicators discussed in his article in this issue, "Measuring
Cycle Periods," can be easily implemented in NeuroShell Trader using NeuroShell
Trader's ability to program functions in standard languages such as C,
C++, Power Basic, or Delphi. A sample NeuroShell chart is shown in Figure
5.
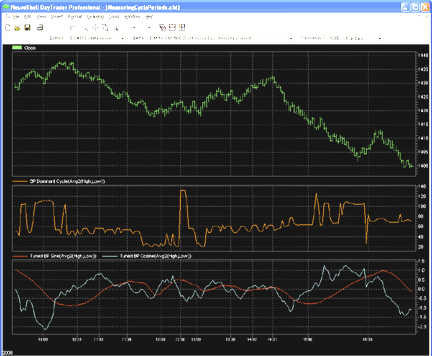
FIGURE 5: NEUROSHELL, EHLERS' CYCLE INDICATORS. This
sample NeuroShell Trader chart shows the dominant cycle indicator and the
dominant cycle-tuned bandpass filter response indicators.
You can recreate Ehlers' bandpass dominant cycle indicator and the
tuned bandpass sine and cosine indicator by moving the EasyLanguage code
provided in Ehlers' article to your preferred compiler and setting up the
corresponding functions. You can insert the resulting indicators as follows:
1. Select "New Indicator ..." from the Insert menu.
2. Choose the Ehlers Band Pass Filter category.
3. Select the bandpass dominant cycle, tuned bandpass sine or cosine
indicators.
4. To match Ehlers' code, change "Price from close" to "Divide (Add2
(High, Low), 2)" from the Arithmetic category.
5. Select the Finished button.
Dynamic trading systems can be easily set up in NeuroShell Trader
by combining the dominant cycle indicators with the adaptive length indicators
available in John Ehlers' Cybernetic and Mesa8 NeuroShell Trader add-ons.
Ehlers suggests that adaptive length indicators linked to the dominant
cycle indicator, when combined with NeuroShell Trader's genetic optimizer,
could produce very robust systems. Similar strategies can also be created
using the dominant cycle indicator found in John Ehlers' Mesa8 NeuroShell
Trader Add-on.
Users of NeuroShell Trader can go to the STOCKS & COMMODITIES section
of the NeuroShell Trader free technical support website to download a copy
of this or any previously published Traders' Tips.
For more information on NeuroShell Trader, visit www.NeuroShell.com.
--Marge Sherald, Ward Systems Group, Inc.
301 662-7950, sales@wardsystems.com
www.neuroshell.com
GO BACK
WORDEN BLOCKS: MEASURING CYCLE PERIODS
To use the study described here, you will need the free Blocks software.
Go to www.Blocks.com to download the software and get detailed information
on the available data packs.
To load the spectrum study that is described by John Ehlers in his article
in this issue, "Measuring Cycle Periods," open Blocks, then click the Indicators
button. Browse to the "SC Traders Tips" folder, then click on "Measuring
Cycle Periods."
The spectrum can be used to analyze any plot, so you'll be prompted
with a dialog to "Add Measuring Cycles to." Click on "price history," then
click OK. Or choose a different plot to analyze. See Figure 6.
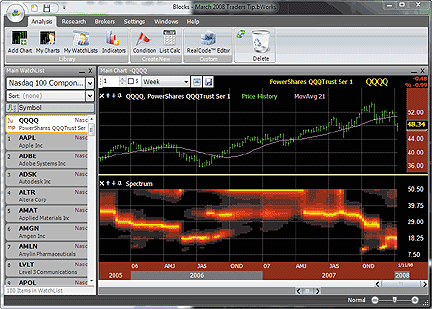
FIGURE 6: WORDEN BLOCKS, EHLERS' CYCLE INDICATORS. The
intensity of the spectrum shows the dominant cycle of the price graph.
To download the Blocks analysis software, go to www.Blocks.com.
To choose your Blocks Analysis Packs, call 800 776-4940 or order online
at the Blocks website.
--Bruce Loebrich and Patrick Argo
Worden Brothers, Inc.
GO BACK
STRATASEARCH: MEASURING CYCLE PERIODS
Based on John Ehlers' article in this issue, "Measuring Cycle Periods,"
we chose to implement the dominant cycle-tuned bandpass filter response
to test Ehlers' suggestion to use the sine and cosine crossovers as buy
and sell signals. If the sine closely follows the price pattern as suggested,
and the cosine is an effective leading function of the sine, then it seems
to make sense that a crossover implementation would work well.
What we discovered in our tests is that crossovers happen at frequent
intervals, even when price has not moved significantly. This leads to a
higher percentage of losing trades, particularly when spread, slippage,
and commissions are accounted for. Nevertheless, the cosine crossover was
quite effective at identifying reversals very early in many cases, so this
indicator could prove quite effective when used alongside other indicators.
In particular, the use of an indicator to confirm a certain level of recent
volatility, as well as an indicator to confirm significant rate of change,
could prove quite helpful.
A sample chart is shown in Figure 7.
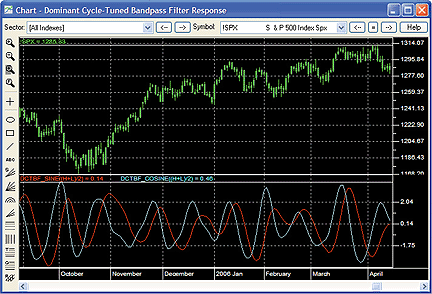
FIGURE 7: STRATASEARCH, DOMINANT CYCLE-TUNED BANDPASS FILTER
RESPONSE. As discussed by John Ehlers in his article in this
issue, the cosine (cyan) component proves to be a helpful leading function
of the sine (red) component.
As with all other Traders' Tips, additional information, including
plug-ins, can be found in the Shared Area of the StrataSearch user forum.
This month's plug-in contains a number of prebuilt trading rules that will
allow you to include this indicator in your automated searches. Simply
install the plug-in and let StrataSearch identify which supporting indicators
might be helpful.
--Pete Rast, Avarin Systems Inc
www.StrataSearch.com
StrataSearch code:
//************************************************************************************
// DOMINANT CYCLE-TUNED BANDPASS FILTER RESPONSE - Sine
//************************************************************************************
DCTBF_API int DCTBF_Sine(Prices *pPrices, Values *pResults, int nTotDays, Values *pValue1) {
double alpha1;
int CurrentBar;
double *Price;
double *HP;
double *SmoothHP;
double delta;
double beta;
double gamma;
double alpha;
int N;
double MaxAmpl;
double Num;
double Denom;
double *DC;
double DomCyc;
double *Value1;
double *Value2;
double Q[51];
double I[51];
double Real[51];
double Imag[51];
double Ampl[51];
double OldQ[51];
double OldI[51];
double OlderQ[51];
double OlderI[51];
double OldReal[51];
double OldImag[51];
double OlderReal[51];
double OlderImag[51];
double OldAmpl[51];
double DB[51];
Price = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(Price, sizeof(double) * nTotDays);
HP = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(HP, sizeof(double) * nTotDays);
SmoothHP = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(SmoothHP, sizeof(double) * nTotDays);
DC = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(DC, sizeof(double) * nTotDays);
Value1 = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(Value1, sizeof(double) * nTotDays);
Value2 = (double *) malloc(sizeof(double) * nTotDays);
ZeroMemory(Value2, sizeof(double) * nTotDays);
for(CurrentBar=0; CurrentBar<nTotDays; CurrentBar++) {
ZeroMemory(Q, sizeof(Q));
ZeroMemory(I, sizeof(I));
ZeroMemory(OldQ, sizeof(OldQ));
ZeroMemory(OldI, sizeof(OldI));
ZeroMemory(OlderQ, sizeof(OlderQ));
ZeroMemory(OlderI, sizeof(OlderI));
ZeroMemory(Real, sizeof(Real));
ZeroMemory(Imag, sizeof(Imag));
ZeroMemory(Ampl, sizeof(Ampl));
ZeroMemory(OldReal, sizeof(OldReal));
ZeroMemory(OldImag, sizeof(OldImag));
ZeroMemory(OlderReal, sizeof(OlderReal));
ZeroMemory(OlderImag, sizeof(OlderImag));
ZeroMemory(OldAmpl, sizeof(OldAmpl));
ZeroMemory(DB, sizeof(DB));
ZeroMemory(DC, sizeof(DC));
Price[CurrentBar] = pValue1[CurrentBar].dValue;
if(CurrentBar == 0) {
pResults[CurrentBar].dValue = 0;
pResults[CurrentBar].chIsValid = 0;
continue;
}
alpha1 = (1 - sin(DegreesToRadians(360/40)))/cos(DegreesToRadians(360/40));
HP[CurrentBar] = .5*(1+alpha1)*(Price[CurrentBar] - Price[CurrentBar-1])+alpha1*HP[CurrentBar-1];
if(CurrentBar >= 6)
SmoothHP[CurrentBar] = (HP[CurrentBar] + 2*HP[CurrentBar-1] + 3*HP[CurrentBar-2]
+ 3*HP[CurrentBar-3] + 2*HP[CurrentBar-4] + HP[CurrentBar-5]) / 12;
if(CurrentBar < 6)
SmoothHP[CurrentBar] = Price[CurrentBar] - Price[CurrentBar-1];
delta = -.015*(CurrentBar+1) + .5;
if(delta < .15)
delta = .15;
if(CurrentBar > 5) {
for(N=8; N<=50; N++) {
beta = cos(DegreesToRadians(360 / N));
gamma = 1 / cos(DegreesToRadians(720*delta / N));
alpha = gamma - sqrt(gamma*gamma - 1);
Q[N] = (N / 6.283185)*(SmoothHP[CurrentBar] - SmoothHP[CurrentBar-1]);
I[N] = SmoothHP[CurrentBar];
Real[N] = .5*(1 - alpha)*(I[N] - OlderI[N]) + beta*(1+ alpha)*OldReal[N] - alpha*OlderReal[N];
Imag[N] = .5*(1 - alpha)*(Q[N] - OlderQ[N]) + beta*(1 + alpha)*OldImag[N] - alpha*OlderImag[N];
Ampl[N] = (Real[N]*Real[N] + Imag[N]*Imag[N]);
}
}
for(N=8; N<=50; N++) {
OlderI[N] = OldI[N];
OldI[N] = I[N];
OlderQ[N] = OldQ[N];
OldQ[N] = Q[N];
OlderReal[N] = OldReal[N];
OldReal[N] = Real[N];
OlderImag[N] = OldImag[N];
OldImag[N] = Imag[N];
OldAmpl[N] = Ampl[N];
}
MaxAmpl = Ampl[10];
for(N=8; N<=50; N++) {
if(Ampl[N] > MaxAmpl)
MaxAmpl = Ampl[N];
}
for(N=8; N<=50; N++) {
if(MaxAmpl != 0 && (Ampl[N] / MaxAmpl) > 0)
DB[N] = -10*log(.01 / (1 - .99*Ampl[N] / MaxAmpl)) / log(10);
if(DB[N] > 20)
DB[N] = 20;
}
Num = 0;
Denom = 0;
for(N=10; N<=50; N++) {
if(DB[N] <= 3) {
Num = Num + N*(20 - DB[N]);
Denom = Denom + (20 - DB[N]);
}
if(Denom != 0)
DC[CurrentBar] = Num / Denom;
}
if(CurrentBar > 9)
DomCyc = Median(&DC[CurrentBar], 10);
if(DomCyc < 8)
DomCyc = 20;
beta = cos(DegreesToRadians(360 / DomCyc));
gamma = 1 / cos(DegreesToRadians(720*delta / DomCyc));
alpha = gamma - sqrt(gamma*gamma - 1);
if(CurrentBar<2) {
pResults[CurrentBar].dValue = 0;
pResults[CurrentBar].chIsValid = 0;
continue;
}
Value1[CurrentBar] = .5*(1 - alpha)*(SmoothHP[CurrentBar] - SmoothHP[CurrentBar-1])
+ beta*(1 + alpha)*Value1[CurrentBar-1] - alpha*Value1[CurrentBar-2];
Value2[CurrentBar] = (DomCyc / 6.28)*(Value1[CurrentBar] - Value1[CurrentBar-1]);
pResults[CurrentBar].dValue = Value1[CurrentBar];
pResults[CurrentBar].chIsValid = 'Y';
}
free(Price);
free(HP);
free(SmoothHP);
free(DC);
free(Value1);
free(Value2);
return 0;
}
--Pete Rast
Avarin Systems Inc
www.StrataSearch.com
GO BACK
STRATEGY DESK: MEASURING CYCLE PERIODS
In this month's Traders' Tips column we'll look at cycles, as discussed
by John Ehlers in his article in this issue, "Measuring Cycle Periods."
Here is a StrategyDesk interpretation. The formulas shown here will
assist you in building an oscillator to help you find cycles in market
data.
We'll start by using a moving average; specifically, a centered moving
average. This concept is not new, but the idea is to choose your desired
length and then shift it to the left on the chart by half the number of
periods used for the average. The end result is that it generally rests
more squarely on top of the market data instead of lagging. Longer averages
will tend not to follow the price action as well as shorter averages.
An example is shown on the chart in Figure 8. A 20-period simple moving
average is overlaid on the S&P 500 and shifted 10 periods to the left.
This is accomplished in StrategyDesk by overlaying a simple moving average
of 20 periods and choosing -10 for the offset amount.
Next we'll create an oscillator using this centered moving average.
This is done on a chart by choosing "Custom Study Wizard" from the Studies
menu and adding the following formula:
Bar[Close,D] / MovingAverage[MA,Close,20,-10,D]
We've chosen to title this "Close to 20-day centered Sma."
Finally, place this newly created oscillator below your chart with a
line across the level at 1 to see positive and negative crossovers. This
is displayed in the chart in Figure 8.
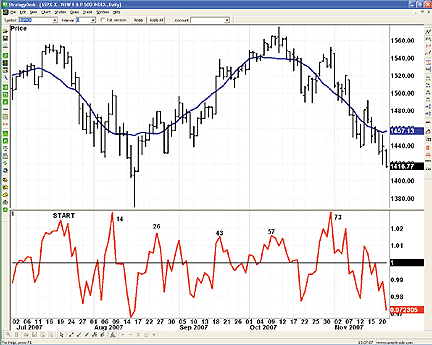
FIGURE 8: TD AMERITRADE, PERIODIC REPETITIONS. The chart
shows the number of periods from the starting point where the upper extremes
have occurred. You can see that cycles have appeared roughly every 14 trading
days.
The next step is to look for periodic repetitions. Using StrategyDesk's
cursor tracking window we can see how many periods have elapsed by simply
clicking and moving the cursor on the chart. Figure 8 shows the number
of periods from the starting point where the upper extremes have occurred.
You'll see that these cycles have appeared roughly every 14 trading days.
This is just one example of finding cycles. If you have questions about
this formula or functionality, please call TD Ameritrade's StrategyDesk
free help line at 800 228-8056, or access the Help Center via the StrategyDesk
application. StrategyDesk is a downloadable application that is free for
all TD Ameritrade clients. Regular commission rates apply.
TD Ameritrade and StrategyDesk do not endorse or recommend any particular
trading strategy.
--Jeff Anderson
TD AMERITRADE Holding Corp.
www.tdameritrade.com
GO BACK
SWINGTRACKER: MEASURING CYCLE PERIODS
We have introduced the BP IQ spectrum indicator into SwingTracker 5.13.088
based on John Ehlers's article in this issue, "Measuring Cycle Periods."
A sample chart is shown in Figure 9.
To discuss these tools, please visit our forum at forum.mrswing.com.
Our development staff can assist your needs at support.mrswing.com.
For information or free trial, visit www.swingtracker.com.
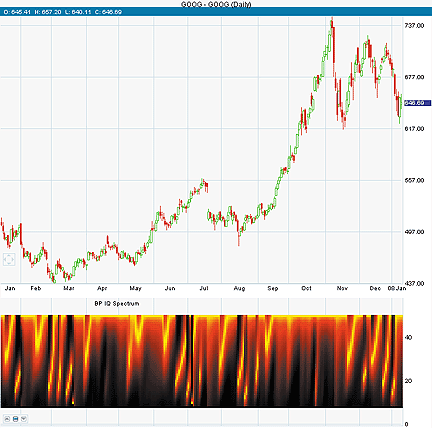
FIGURE 9: SWINGTRACKER, EHLERS' SPECTRUM INDICATORS.
Here is a demonstration of the BP IQ spectrum indicator.
--Larry Swing
theboss@mrswing.com
www.mrswing.com
Code for SwingTracker
SpectrumDSRenderer.java
package com.iqpartners.chart.render;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.RenderingHints;
import java.awt.Color;
import com.iqpartners.data.DataSet;
public class SpectrumDSRenderer extends DataSetRenderer {
/** Constructor */
public SpectrumDSRenderer() {
}
/**
* Draw a histogram
*/
@Override
public void plot(RendererContext rc, DataSet dsRed, DataSet dsGreen, Graphics g) {
Graphics2D g2 = (Graphics2D) g.create();
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
Float[] red = dsRed.getData();
Float[] green = dsGreen.getData();
for (int i = 0; i < red.length; i++) {
if (red[i] != null) {
int y = rc.getY(dsRed.getLevel());
int h = rc.getY(dsRed.getLevel() - 1) - rc.getY(dsRed.getLevel())+1;
int x = rc.getX(i);
g2.setColor(new Color((int) (red[i].floatValue()), (int) (green[i].floatValue()), 0));
float w = rc.getTickWidth(i) + 2;
g2.fillRect(x - (int) Math.round(w / 2), y - (int) Math.round(h / 2), (int) Math.round(w), h);
}
}
}
}
BPIQSpectrumIndicator.java
package com.iqpartners.data.indicator;
import java.awt.Graphics;
import com.iqpartners.chart.render.RangeRenderer;
import com.iqpartners.chart.render.RendererContext;
import com.iqpartners.main.ColorSchemeManager;
import com.iqpartners.data.DataSet;
import com.iqpartners.data.Range;
import com.iqpartners.chart.ChartUtil;
import com.iqpartners.chart.render.SpectrumDSRenderer;
import com.iqpartners.main.TranslatedMessages;
import java.util.ResourceBundle;
public class BPIQSpectrumIndicator extends Indicator {
@Override
protected void setParameters() {
// Initiliaze localization
ResourceBundle messages;
TranslatedMessages translatedMessages = TranslatedMessages.instance();
messages = translatedMessages.getBundle();
setRangeRenderer(new RangeRenderer() {
/**
* Draw the Y Axis
*/
public void plot(RendererContext rc, Range r, Graphics g) {
drawDefaults(rc, g);
// Initiliaze localization
ResourceBundle messages;
TranslatedMessages translatedMessages = TranslatedMessages.instance();
messages = translatedMessages.getBundle();
ChartUtil.setChartLabelFont(g);
int fontDelta = g.getFont().getSize() / 2 - 1;
float tickVal;
String label;
if (r.getHigh() >= 1) {
tickVal = 0;
label = "0";
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
int step = (int) (r.getHigh() / 3) + 1;
for (int i = step; i <= r.getHigh(); i += step) {
tickVal = (float) i;
label = Integer.toString(i);
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
tickVal = (float) -1F * i;
label = Integer.toString(-1 * i);
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
}
} else {
tickVal = 0;
label = "0";
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
float step = (r.getHigh() > 0.5) ? 0.2F : 0.1F;
for (float i = step; i <= r.getHigh(); i += step) {
tickVal = i;
label = Float.toString(i);
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
tickVal = -1F * i;
label = Float.toString(-1 * i);
g.setColor(ColorSchemeManager.current().label());
g.drawString(label, rc.getXMax() + fontDelta + 1, rc.getY(tickVal) + fontDelta);
g.setColor(ColorSchemeManager.current().grid());
g.drawLine(rc.getXMin(), rc.getY(tickVal), rc.getXMax() - 3, rc.getY(tickVal));
}
}
drawTitle(g, rc, getOverlayName());
drawLastLabel(g, rc);
}
});
}
/**
* Recalculate the values for this overlay
*/
protected void calculate() {
clearDataSets();
if ((chartData == null) || chartData.isEmpty()) {
return;
}
DataSet closeDS = DataSet.Close(chartData);
Float[] price = closeDS.getAllData();
DataSet[] plots = new DataSet[51];
DataSet Color1[] = new DataSet[51];
DataSet Color2[] = new DataSet[51];
for (int i = 8; i <= 50; i++) {
plots[i] = new DataSet(chartData);
Color1[i] = new DataSet(chartData);
Color2[i] = new DataSet(chartData);
for (int j = 0; j < price.length; j++) {
plots[i].addFloat((float) i, j);
}
}
DataSet HP = new DataSet(chartData);
DataSet SmoothHP = new DataSet(chartData);
DataSet DC = new DataSet(chartData);
Float[] Q = new Float[51];
Float[] I = new Float[51];
Float[] Real = new Float[51];
Float[] Imag = new Float[51];
Float[] Ampl = new Float[51];
Float[] OlderI = new Float[51];
Float[] OldI = new Float[51];
Float[] OlderQ = new Float[51];
Float[] OldQ = new Float[51];
Float[] OlderReal = new Float[51];
Float[] OldReal = new Float[51];
Float[] OlderImag = new Float[51];
Float[] OldImag = new Float[51];
Float[] OldAmpl = new Float[51];
Float[] DB = new Float[51];
for (int i = 0; i < price.length; i++) {
if (i == 0) {
SmoothHP.addFloat(0.0f, 0);
HP.addFloat(0.0f, 0);
} else if (i < 6) {
double smoothHP = price[i] - price[i - 1];
SmoothHP.addFloat((float) smoothHP, i);
HP.addFloat(0.0f, i);
} else {
double alpha1 = (1.0 - Math.sin(Math.PI / 20.0)) / Math.cos(Math.PI / 20.0);
double hp = 0.5 * (1.0 + alpha1) * (price[i] - price[i - 1]) + alpha1 * HP.dataAtAll(i - 1);
HP.addFloat((float) hp, i);
double smoothHP = (HP.dataAtAll(i) + 2.0 * HP.dataAtAll(i - 1) + 3.0 * HP.dataAtAll(i - 2)
+ 3.0 * HP.dataAtAll(i - 3) + 2.0 * HP.dataAtAll(i - 4)
+ HP.dataAtAll(i - 5)) / 12.0;
SmoothHP.addFloat((float) smoothHP, i);
}
double delta = -0.015 * i + 0.5;
if (delta < 0.15) {
delta = 0.15;
}
if (i > 5) {
for (int n = 8; n <= 50; n++) {
float beta = (float) Math.cos((2.0 * Math.PI) / n);
float gamma = (float) (1.0 / Math.cos((4.0 * Math.PI) / n));
float alpha = (float) (gamma - Math.sqrt(gamma * gamma - 1.0));
Q[n] = (n / 6.283185f) * (SmoothHP.dataAtAll(i) - SmoothHP.dataAtAll(i - 1));
I[n] = SmoothHP.dataAtAll(i);
if (I[n] == null) {
I[n] = 0.0f;
}
if (Q[n] == null) {
Q[n] = 0.0f;
}
Real[n] = (float) (0.5 * (1.0 - alpha) * (I[n] - OlderI[n])
+ beta * (1.0 + alpha) * OldReal[n] - alpha * OlderReal[n]);
Imag[n] = (float) (0.5 * (1.0 - alpha) * (Q[n] - OlderQ[n])
+ beta * (1.0 + alpha) * OldImag[n] - alpha * OlderImag[n]);
Ampl[n] = Real[n] * Real[n] + Imag[n] * Imag[n];
}
} else {
for (int n = 8; n <= 50; n++) {
float beta = (float) Math.cos((2.0 * Math.PI) / n);
float gamma = (float) (1.0 / Math.cos((4.0 * Math.PI) / n));
float alpha = (float) (gamma - Math.sqrt(gamma * gamma - 1.0));
Q[n] = 0.0f;
I[n] = 0.0f;
OlderI[n] = 0.0f;
OlderQ[n] = 0.0f;
OldReal[n] = 0.0f;
OlderReal[n] = 0.0f;
OldImag[n] = 0.0f;
OlderImag[n] = 0.0f;
Real[n] = (float) (0.5 * (1.0 - alpha) * (I[n] - OlderI[n])
+ beta * (1.0 + alpha) * OldReal[n] - alpha * OlderReal[n]);
Imag[n] = (float) (0.5 * (1.0 - alpha) * (Q[n] - OlderQ[n])
+ beta * (1.0 + alpha) * OldImag[n] - alpha * OlderImag[n]);
Ampl[n] = Real[n] * Real[n] + Imag[n] * Imag[n];
}
}
for (int n = 8; n <= 50; n++) {
OlderI[n] = OldI[n];
OldI[n] = I[n];
OlderQ[n] = OldQ[n];
OldQ[n] = Q[n];
OlderReal[n] = OldReal[n];
OldReal[n] = Real[n];
OlderImag[n] = OldImag[n];
OldImag[n] = Imag[n];
OldAmpl[n] = Ampl[n];
}
float MaxAmpl = Ampl[10];
for (int n = 10; n <= 50; n++) {
if (Ampl[n] > MaxAmpl) {
MaxAmpl = Ampl[n];
}
}
for (int n = 8; n <= 50; n++) {
if ((MaxAmpl != 0) && (Ampl[n] / MaxAmpl > 0)) {
DB[n] = (float) (-10.0 * Math.log(0.01 / (1 - 0.99 * Ampl[n] / MaxAmpl)) / Math.log(10));
} else {
DB[n] = 0.0f;
}
if (DB[n] > 20) {
DB[n] = 20.0f;
}
}
float Num = 0.0f;
float Denom = 0.0f;
for (int n = 8; n <= 50; n++) {
if (DB[n] <= 3) {
Num = Num + n * (20 - DB[n]);
Denom = Denom + (20 - DB[n]);
}
if (Denom != 0.0f) {
DC.addFloat(Num / Denom, i);
}
}
for (int n = 8; n <= 50; n++) {
if (DB[n] <= 10) {
Color1[n].addFloat(255.0f, i);
float color = 255 * (1 - DB[n] / 10);
Color2[n].addFloat(color, i);
} else {
float color = 255 * (2 - DB[n] / 10);
Color1[n].addFloat(color, i);
Color2[n].addFloat(0.0f, i);
}
}
}
DataSet DomCyc = DataSet.SMA(DC, 10);
for (int n = 8; n <= 50; n++) {
Color1[n].setLevel(n);
Color1[n].setDataSetRenderer(new SpectrumDSRenderer());
addDataSetPair("DS_" + Integer.toString(n), Color1[n], Color2[n]);
}
calculateHigh();
calculateLow();
}
@Override
public void calculateHigh() {
high = 50;
}
@Override
public void calculateLow() {
low = 8;
}
public String getOverlayName() {
// Initiliaze localization
ResourceBundle messages;
TranslatedMessages translatedMessages = TranslatedMessages.instance();
messages = translatedMessages.getBundle();
return messages.getString("bp_iq_spectrum");
}
}
GO BACK
GECKO SOFTWARE: MEASURING CYCLE PERIODS
As discussed in John Ehlers' article in this issue, "Measuring Cycle
Periods," it is well known and well documented that one of the greatest
advantages of trading the commodities market is the fact that they move
in such strong definable cycles through measured periods.
For the year 2007, gold traders who followed the historical seasonal
cycle through the previous year's time frame would have profited significantly
if they took advantage of this single most important phenomenon.
In the sample Track 'n Trade futures chart in Figure 10, the graph at
the bottom of the screen is a representation of the past 10-year price
cycle in blue, with the 15-year price cycle in red as the overlay. In this
graph, we can see that the overall 10- and 15-year historical cycle indicates
that the price of gold has a historically strong rally starting in early
September of each year. As a gold trader, we look forward to this rally
as a regular occurrence, with this past year being no different. As we
see from the price chart, the price of gold continued to rally throughout
the remainder of the year, as it has traditionally done during years past,
as represented by the historical price average indicator. Looking forward
in time, we also see that gold tends to rally through the year all the
way into February of the following year before finding any kind of price
relief.
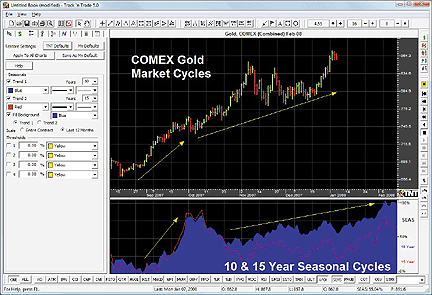
FIGURE 10: GECKO SOFTWARE, 10-YEAR AND 15-YEAR HISTORICAL
CYCLES. Here is a demonstration of historical seasonal cycles of the
gold market in Track 'n Trade.
Track 'n Trade allows the trader to manage and modify the historical time
frames from within the left-pane control panel, giving the user the ability
to manipulate the data in a number of different ways. As seen in this example,
we have chosen to see the 10-year historical cycle represented in blue
and the 15-year represented in red. Track 'n Trade also has the ability
to activate historical price averages as an overlay, directly in reference
to price, also available from the left-pane control panel.
--Lan H. Turner
www.geckosoftware.com
GO BACK
AIQ: CONFIRMING PRICE TREND
The AIQ code for the set of indicators that Barbara Star discusses in
her December 2007 article, "Confirming Price Trend," is shown here. Figure
11 shows the two linear regression indicators plotted on a chart of Express
Scripts.
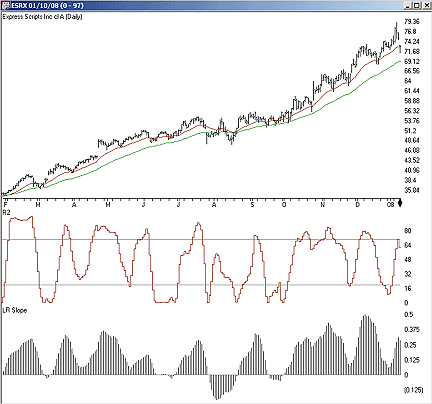
FIGURE 11: AIQ, LINEAR REGRESSION INDICATORS. Here,
the linear regression indicators r-squared and linear regression slope
for a 20-day period are shown on a chart of Express Scripts.
This code can be downloaded from the AIQ website at www.aiqsystems.com
and also from www.tradersedge systems.com/traderstips.htm.
! CONFIRMING PRICE TREND
! Author: Barbara Star, TASC Dec 2007
! Coded by: Richard Denning 01/07/08
C is [close].
C1 is valresult(C,1).
C2 is valresult(C,2).
C3 is valresult(C,3).
C4 is valresult(C,4).
C5 is valresult(C,5).
C6 is valresult(C,6).
C7 is valresult(C,7).
C8 is valresult(C,8).
C9 is valresult(C,9).
C10 is valresult(C,10).
C11 is valresult(C,11).
C12 is valresult(C,12).
C13 is valresult(C,13).
C14 is valresult(C,14).
C15 is valresult(C,15).
C16 is valresult(C,16).
C17 is valresult(C,17).
C18 is valresult(C,18).
C19 is valresult(C,19).
! CONSTANTS FOR N = 20:
! N = 20.
! SUM_X = 210.
! SUM_X*SUM_X = 44100.
! SUM_X2 = 2870.
SUM_Y is sum(C,20).
SUM_XY is C19 + 2*C18 + 3*C17 + 4*C16 + 5*C15 + 6*C14 + 7*C13
+ 8*C12 + 9*C11 + 10*C10 + 11*C9 + 12*C8 + 13*C7 + 14*C6
+ 15*C5 + 16*C4 + 17*C3 + 18*C2 + 19*C1 + 20*C.
SUM_Y2 is sum(C*C,20).
R is ((20*SUM_XY-210*SUM_Y)
/ sqrt((20*2870-44100)*(20*SUM_Y2-SUM_Y*SUM_Y))).
R2 is R*R.
! INDICATORS TO PLOT:
! R2 TIMES 100:
PlotR2 is R2 * 100.
! LINEAR REGRESSION SLOPE INDICATOR
LRS20 is slope2(C,20).
--Richard Denning, AIQ Systems
richard.denning@earthlink.net
GO BACK
VT TRADER: ANGLE OF ASCENT INDICATOR
For this month's Traders' Tip, we're revisiting an article by Martha
Stokes from the September 2007 issue of S&C titled "The Angle Of Ascent."
In that article, Stokes discusses the merits of determining the angle at
which price is ascending or descending to better pinpoint trade entries.
She goes on to mention that the ideal angle of ascent is 45 degrees on
the most recent price action.
For our purposes, we'll use the linear regression indicator, which can
be found in VT Trader, as the basis for determining the angle of ascent.
The VT Trader code and instructions for recreating the angle of ascent
indicator are as follows:
Angle of ascent indicator
1. Navigator Window>Tools>Indicator Builder>[New] button
2. In the Indicator Bookmark, type the following text for each field:
Name: TASC TASC - 03/2008 - Angle of Ascent Indicator
Short Name: vt_AofA
Label Mask: TASC - 03/2008 - Angle of Ascent Indicator (LRI: %RegPeriods%, %Price%,
LRI Pre-Smoothing: %SmoothPeriods%, %SmoothType% | Slope Periods: %slopeper%)
Placement: New Frame
Inspect Alias: Angle of Ascent Indicator
3. In the Input Bookmark, create the following variables:
[New] button... Name: RegPeriods , Display Name: Regression Periods , Type: integer , Default: 8
[New] button... Name: Price , Display Name: Regression Price , Type: price , Default: close
[New] button... Name: SmoothPeriods , Display Name: Pre-Smoothing Price Periods , Type: integer , Default: 1
[New] button... Name: SmoothType , Display Name: Pre-Smoothing MA Type , Type: MA type , Default: Simple
[New] button... Name: slopeper , Display Name: Slope Periods , Type: integer , Default: 8
4. In the Output Bookmark, create the following variables:
[New] button...
Var Name: Degrees
Name: (Degree of Angle)
Line Color: dark green
Line Width: slightly thicker
Line Type: solid
5. In the Horizontal Line Bookmark, create the following variables:
[New] button...
Value: +45.0000
Color: red
Width: thin
Style: dashed line
[New] button...
Value: +0.0000
Color: black
Width: thin
Style: dashed line
[New] button...
Value: -45.0000
Color: red
Width: thin
Style: dashed line
6. In the Formula Bookmark, copy and paste the following formula:
{Provided By: Visual Trading Systems, LLC & Capital Market Services, LLC (c) Copyright 2008}
{Description: Angle of Ascent Indicator}
{Notes: T.A.S.C., September 2007 - "The Angle of Ascent" by Martha Stokes}
{vt_AofA Version 1.0}
{Calculate Linear Regression Indicator}
SmoothData:= mov(Price,SmoothPeriods,SmoothType);
LRI:= linreg(SmoothData,RegPeriods);
{Determine the Angle of Ascent of LRI}
NormalizedDifferenceInPrice:= if(SymbolPoint()=0.0001,10000,100);
Rise:= (LRI - ref(LRI,-slopeper)) * NormalizedDifferenceInPrice;
Run:= slopeper;
Slope:= Rise/Run;
Angle:= atan(Slope);
Degrees:= Angle * 180 / PI;
7. Click the "Save" icon to finish building the angle of ascent indicator.
To attach the indicator to a chart (Figure 12), click the right mouse
button within the chart window and then select "Add Indicators" -> "TASC
- 03/2008 - Angle of Ascent Indicator" from the indicator list.
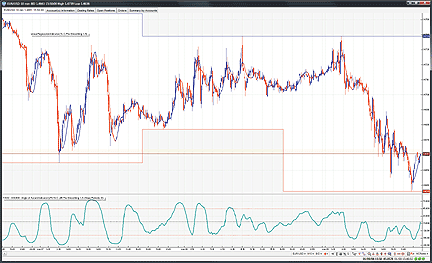
FIGURE 12: VT TRADER, LINEAR REGRESSION AND ANGLE OF ASCENT.
Here is the angle of ascent indicator displayed over a EUR/USD 10-minute
candlestick chart.
To learn more about VT Trader, please visit www.cmsfx.com.
--Chris Skidmore
CMS Forex
(866) 51-CMSFX, trading@cmsfx.com
www.cmsfx.com
GO BACK
Return to March 2008 Contents
Originally published in the March 2008 issue of Technical Analysis
of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright
2008, Technical Analysis, Inc.
![]() TRADESTATION: MEASURING CYCLE PERIODS
TRADESTATION: MEASURING CYCLE PERIODS
![]() eSIGNAL: MEASURING CYCLE PERIODS
eSIGNAL: MEASURING CYCLE PERIODS
![]() WEALTH-LAB: MEASURING CYCLE PERIODS
WEALTH-LAB: MEASURING CYCLE PERIODS
![]() AMIBROKER: MEASURING CYCLE PERIODS
AMIBROKER: MEASURING CYCLE PERIODS
![]() NEUROSHELL TRADER: MEASURING CYCLE PERIODS
NEUROSHELL TRADER: MEASURING CYCLE PERIODS
![]() WORDEN BLOCKS: MEASURING CYCLE PERIODS
WORDEN BLOCKS: MEASURING CYCLE PERIODS
![]() STRATASEARCH: MEASURING CYCLE PERIODS
STRATASEARCH: MEASURING CYCLE PERIODS
![]() STRATEGY DESK: MEASURING CYCLE PERIODS
STRATEGY DESK: MEASURING CYCLE PERIODS
![]() SWINGTRACKER: MEASURING CYCLE PERIODS
SWINGTRACKER: MEASURING CYCLE PERIODS
![]() GECKO SOFTWARE: MEASURING CYCLE PERIODS
GECKO SOFTWARE: MEASURING CYCLE PERIODS
![]() AIQ: CONFIRMING PRICE TREND
AIQ: CONFIRMING PRICE TREND
![]() VT TRADER: ANGLE OF ASCENT INDICATOR
VT TRADER: ANGLE OF ASCENT INDICATOR











