Editor,
I found John Ehlers' article in the March 2008 S&C, "Measuring Cycle Periods," a very interesting way to adjust my indicators. But I have a question: How do I find out what the dominant cycle is, and how do I calculate it? I am asking because this is the key thing to start with.
Klemen Vatovec
Slovenia
John Ehlers replies:
The default setting to display the dominant cycle is False, as shown in the third line of code on page 18 of the March 2008 issue. When run in TradeStation, this input is easily changed to True so the dominant cycle is plotted as an overlay on the spectrum. When using the dominant cycle to adjust other indicators, I suggest using half of the dominant cycle period for oscillators such as the RSI or stochastics, where a peak-to-valley swing is desired. On the other hand, one should use the full dominant cycle period for determining the true slope of a trend by taking a momentum over the full period, or for indicators such as the CCI to determine a trading channel.
Editor: For more on finding cycles, see some of John Ehlers' past articles in S&C by using the search feature at our website, Traders.com, to locate them. Here are just a few articles to mention:
"When To Trade With Cycles" (April 2007)
by John F. Ehlers
When should you trade the cycle mode in a market and when should you
trade the trend mode?
"Fourier Transform For Traders" (January 2007)
by John F. Ehlers
When market conditions are variable, adapting to them becomes a challenge.
Here's how you can use a dominant cycle to tune the relevant indicators.
"Modeling The Market = Building Trading Strategies" (August
2006)
by John F. Ehlers
The right model can form the foundation for comprehensive trading strategies.
"Cycle Measurements" (November 1997)
by John F. Ehlers
The author of MESA and Trading Cycles and developer of the MESA software
series presents why you should dynamically adjust your indicators due to
the change in market cycles.
"Do Cycles Exist In The Market?" (September 1997)
by John F. Ehlers
This longtime S&C contributor explains the basis of the existence
of cycles in market data.
"Stay In Phase" (November 1996)
by John F. Ehlers
This cycles software specialist discusses an indicator based on cyclical
analysis. Includes BASIC code for phase calculation.
"Understanding Cycles" (July 1985)
by John F. Ehlers
In this article, we will go back to basics and briefly review cycle
theory to have a common basis for definitions.
TRADING FLOOR AUDIO
Editor,
I am a new subscriber. As a former floor trader, I would like to find audio software to abet electronic trading. I will be using a Bloomberg machine and CQG. What suggestions have you?
Erik Hooks
See our reviews of TradeTheNews.com, TradersAudio.com, and NeedToKnowNews.com:
Gopalakrishnan, Jayanthi [2005]. "TradeTheNews.com," Quick-Scan,
Technical Analysis of STOCKS & COMMODITIES, Volume 24: March.
Penn, David [2006]. "News Traders Can Use: TradersAudio.com and
NeedToKnowNews.com," Websites For Traders, Technical Analysis of
STOCKS & COMMODITIES, Volume 24: December.
There are several other services as well that you may be able to find over the Internet, although we have not reviewed them.--Editor
HISTORICAL DATA
Editor,
I was wondering if you knew of a source of historical data for stocks (open/high/low/close) during the years 1908-09, as well as data for some commodities such as cotton and wheat. I wanted to look at the same markets that W.D. Gann looked at in his newsletters.
James
You might try www.topline-charts.com. This company seems to have a good collection of historical data going back as far as 1908.--Editor
GETTING STARTED IN TECHNICAL ANALYSIS
Editor,
I just started subscribing to STOCKS & COMMODITIES after picking up a few issues off the newsstand. I am looking for some basic advice on getting started in technical analysis, for example, which platforms should I look into, which indicators are the most useful, and so on.
M.N.
You can start with a low-cost or free website that offers stock charting and/or try out some free trials on other charting programs or technical analysis products to start getting a feel for charting the markets. After you start to develop an approach to the markets that suits you and after gaining some of the necessary skills to trade, you'll have a better idea of what type of product or platform would be most useful for you. Platforms range from straightforward to customizable and programmable, and they can specialize in different approaches to market analysis.
See also the Readers' Choice Awards in our Bonus Issue (which was mailed to subscribers last month and is mailed to new subscribers throughout the year) for the products that our readers tell us they are using and like, and especially see the category of "Subscription Internet analytical platforms." For lists (though not ratings) of many additional products, see the Traders' Resource database at our website, www.Traders.com. Also at our website, you'll find a Novice Trader's Notebook section with explanatory entries on different charting patterns.
There are also many books available as primers for technical analysis. Good luck!--Editor
ERRATA: SVAPO PRICE-ONLY INDICATOR METASTOCK CODE
In the article "Trading Medium-Term Divergences" by Vervoort Sylvain published in the February 2008 issue, an error occurred in the "SVAPO price only indicator for MetaStock" sidebar on page 21.
In the MetaStock code, the following segment of code:
{calculate heikin ashi closing average haCI and get the input variables}haO:=(Ref((O+H+L+C)/4,-1)+PREV)/2;haC:=((O+H+L+C)/4+haOpen+Max(H,haOpen)+ Min(L,haOpen))/4;
should be replaced with:
{calculate heikin ashi closing average haCl and get the input variables}haOpen:=(Ref((O+H+L+C)/4,-1)+PREV)/2;haCl:=((O+H+L+C)/4+haOpen+Max(H,haOpen)+ Min(L,haOpen))/4;
STOCK MARKET HISTORY
Editor,
As a reader of your magazine, I would like to congratulate you for the very interesting article by Mark Vakkur in your January 2008 issue, "What Works, What Doesn't In Stock Market History," which I enjoyed. It made me want to read the follow-up article.
The study relies on the correlation between starting dividend/earnings yields and subsequent returns from the S&P 500 in order to establish some predictability property to the former (often a fallacious use of correlation, but one that I think is fair to assume in this study).
Correlation is a measure of strength and direction of linear dependence between two variables, and its value may not be sufficient to evaluate that dependence if the assumption of normality of the deviations from linearity is not valid. Therefore, it would be advisable to provide scatter plots of the data to visually inspect them for linearity, thus attesting the correlation suitableness.
In addition, correlations of 66-68% (the highest of the test) still leave one-third of the S&P returns unexplained by the dividend/earnings factors, which does not provide the strongest support to that predictability assumption.
The article also contains some minor errors, specifically related to statistical concepts, that I would like to point out:
1. On page 29, Mr. Vakkur writes, "... the standard deviation [...] implies a normal distribution." Standard deviation, by itself, has no implication on the distribution form. It is just a measure of dispersion about the mean, derived from the mean square deviation (the second central moment of the distribution).
2. Frequently, Mr. Vakkur refers to the 50% percentile as the average when, in fact, it is the median (though they match in a perfect normal distribution).
All this said, the article remains a very interesting one and I look forward to the second part.
Marco Alves
Editor's note: Mark Vakkur was intrigued by this question from Marco Alves and went into great detail when giving his response. He consulted with his sister, Justine Shults, PhD, professor of biostatistics at the University of Pennsylvania for his response, which can be found below.
From Marco Alves's letter: The study relies on the correlation between starting dividend/earnings yields and subsequent returns from the Standard & Poor's 500 in order to establish some predictability property to the former (often a fallacious use of correlation, but one that I think is fair to assume in this study).
The research showing correlation between dividend yields and earnings yield both for individual stocks and for broad stock market indexes is extensive. I would refer the writer to the work of John Bogle, founder of the Vanguard Funds, an early index fund proponent. In his book Bogle On Mutual Funds, he provided extensive historical data showing that from 1926 to 1992 (in this case), the biggest predictor of stock market returns over any given decade was the dividend yield of the stock market at the beginning of the decade. Further, he gives one of the most cogent explanations of why this must be so, namely that dividends form the lion's share of stock returns over time (even a modest dividend yield reinvested in the asset throwing off the dividend will compound geometrically), that dividends have historically grown at about 4.8% a year, and that aberrantly high or low dividend yields tend to regress to a mean, giving an additional kick to an investor who buys when prices are low relative to dividends. This is assuming that correlation between dividends and subsequent returns, as the reader agrees, is "fair to assume" in this study.
At any rate, since dividends are by definition part of total return (although in fairness, I looked mostly at changes in the S&P 500 excluding dividends), it should be no surprise that dividend yield would be correlated with subsequent return. This observation, of course, must be tempered with the observation that extremely high dividend yields sometimes signal a company in distress that must be forced to slash or eliminate the dividend, and that may suffer a loss in share price that would offset dividends collected during the holding period. Establishing correlation is not necessary if the independent variable is part of the dependent variable; the question is only whether an efficient market corrects for aberrantly high or low dividends, "correctly" driving down share prices of distressed companies (or a distressed market of stocks) to reflect poor future returns. The historical record seems an unequivocal no; investors who drive down share prices, driving up yields, have overshot to the downside. Conversely, optimistic investors who drive share prices up to excessively relative to dividend yields are incorrect in their assumption that paltry dividend yields will be offset by proportionally greater returns from capital gains.
If markets correctly and efficiently discounted stocks to a price appropriate for prevailing interest rates, economic outlook, company, sector, and market-specific factors, and so forth, then any predictive value provided by historically high or low dividend yields should be stripped away (for example, the correlation should be zero). All of the comments made regarding dividends are true, although indirectly, for earnings and book value. Since dividends ultimately are paid out of cash flow and earnings, buying stocks with historically high earnings yield has led to historically above-average subsequent total returns.
Correlation is a measure of strength and direction of linear dependence between two variables, and its value may not be sufficient to evaluate that dependence if the assumption of normality of the deviations from linearity is not valid. Therefore, it would be advisable to provide scatter plots of the data to inspect them for linearity, thus attesting the correlation suitableness.
We agree that it would have been preferable to obtain correlations that are closer to 1.00 in value. In fact, a correlation of 0.68 indicates that 46% of the variability in S&P returns is explained by the dividend/earning factors, so that 54% of the variance is unexplained by our model. (The 46% corresponds to the r-squared value in a simple linear regression of S&P returns on dividends/earning factors, which is calculated as the square of the correlation.)
While a higher correlation is always desirable, depending on the outcome, it can be difficult to achieve. Given the volatility and difficulty in predicting S&P returns, a model that explains almost half of the variability in these returns may be quite promising. This correlation for a single variable is in line with what other authors have found.
Marco Alves is adding a level of complexity to this analysis that I believe may create a less robust model of market returns than using an empirical observation stripped of any assumptions of either linearity or normal distribution or both.
Two variables can be correlated but in a nonlinear way, for example, age and height. The average six-year-old is taller than the average three-year-old, but this does not mean that the average 60-year-old is taller than the average 30-year-old, or that the ratio between the height of the three-year-old and the six-year-old tells you anything meaningful about the ratio of the height of the 60-year-old to the 30-year-old. In fact, as we age, we may lose height to the forces of osteoporosis, so the average 80-year-old may be shorter than the average 60-year-old. However, it is also incorrect to assume that because this relationship is nonlinear, it is useless. If we construct a table of age versus average height with distributions of height, we can make some determinations of height at some future date without making any assumptions about linearity, covariance, or correlation.
My attempt in the article was to provide a sort of growth chart for the stock market, dividing the data into buckets by quartile then averaging each of those buckets, making no assumptions about the distributions within or between those buckets.
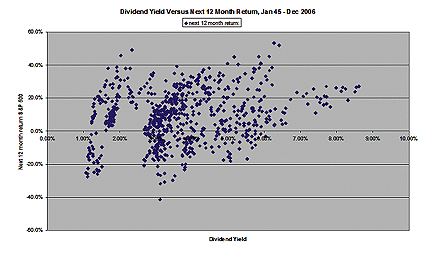
The scatter plot in Figure 1 shows 12-month returns versus the dividend yield at the start of the period. As with any financial series, it is noisy with some high-return periods following low-dividend yields and some low returns following modest or moderately high-dividend yields, but the following is clear:
• When the dividend yield exceeded 6.04%, there were
no subsequent 12-month losing periods in the stock market
• When the dividend yield exceeded 3.82%, there were
no S&P 500 declines of 20% or more
• Two clusters of negative returns jump out: at around
modestly above-average dividend yields and extremely above-average dividend
yields.
FIGURE 1: SCATTERPLOT: 12-month return vs. dividend yield
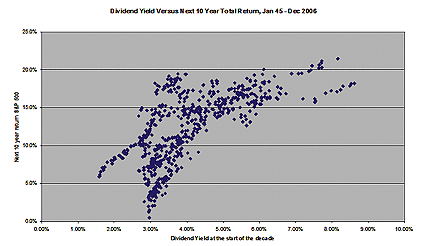
FIGURE 2: SCATTERPLOT: 10-year observation period
This relationship becomes even more clear if the observation period
is extended to 10 years (Figure 2). (The return data is annualized.)
A positive relationship between starting dividend yield and subsequent total return is visually apparent, with no dividend yields below 4.32% returning less than 10% a year over the next decade, and no periods beginning with a 3.13% yield or lower seeing subsequent average annual returns of more than 15%. All but one of the 20%-plus decades were preceded by beginning dividend yields of more than 7.5%. All decades that started with a dividend yield of 2.45% or below had average returns of less than 10%.
It also seems clear that high dividend yields have better positive predictive power than low dividend yields have negative predictive power. In other words, we can have much more confidence that high returns will follow very high dividend yields than that low or substandard returns will follow low dividend yields.
In addition, correlations of 66% to 68% (the highest of the test) still leave one-third of the S&P returns unexplained by the dividend/earnings factors, which does not provide the strongest support to that predictability assumption.
I have looked at many financial data series and have never seen correlation coefficients approaching anywhere close to 0.66-0.68. Financial data series are always noisy probably because of two major factors: First, there are multiple inputs and covariance of inputs so looking at one variable in isolation will only give a piece of the picture; and second, how those inputs are discounted and responded to by the human participants who make up the markets changes over time in magnitude (although I would argue the direction of the discounting is similar -- for example, low interest rates are most often correlated with higher stock returns, but the degree of rate reduction that must correspond to a given change in stocks may change with time, macroeconomic conditions, overall pessimism versus optimism, where we are in the business cycle, and whether the business cycle is capital or commodity intensive, and so on). I do not believe this noise can ever be successfully eliminated.
Standard deviation, by itself, has no implication on the distribution form. It is just a measure of dispersion about the mean, derived from the mean square deviation (the second central moment of the distribution).
This is technically correct but a standard deviation is generally assumed (correctly or incorrectly) by most investors to mean that a distribution is normally distributed. If I tell you that the stock market has a 21% average annual standard deviation, you may invest with the false confidence that two-thirds of all subsequent returns should be 21% above or below the mean, and only once every few centuries should the market deviate by more than three times its standard deviation from the mean. All of these assumptions infer a normal distribution, so reporting a standard deviation without that caveat could be misleading. As it turns out, the market's tails are much fatter than a standard deviation would imply. I use standard deviation only as a rough gauge of how dispersed data are, reminding myself that I always assume my distribution is nonparametric.
Frequently, Mr. Vakkur refers to the 50% percentile as the average when, in fact, it is the median (though they match in a perfect normal distribution).
Interestingly, this is a pet peeve of mine, so I searched in vain for the reference Mr. Alves is making. It is true that I "frequently" used the word average, but in every instance I could find, it referred either to the mean or to the bottom half of the sample. Both are correct usages. If the median and mean annual income of a group of men in a bar is $100,000, let's say, and Bill Gates walks in, chances are the mean would shift dramatically, whereas the median would be no more affected (depending on whether there were an odd or even number of men to begin with and what values clustered around the middle of the sample) than if someone walked in with an annual income of $101,000.
Assuming that the mean has shifted to a value that exceeds everyone in the room except Bill Gates, is it really meaningful (no pun intended) to talk about everyone in the bar having a below-average income? Or is this understood in common parlance to mean those in the bottom two quartiles (below median)? Similarly, if the median dividend yield is 3.5% (the mean is 3.71%), I believe it is more understandable to describe the 50% of months in the sample when the dividend yield was less than 3.5% as "below average" instead of the more cumbersome "below median" or "lowest two quartiles." Technically speaking, 56.4% of the sample was "below average" if we insist on meaning only "below the arithmetic mean" but the larger points made in the article (and generalizations about the dataset) are unaffected.
The dependent variable I was studying was a mean (average) return given a quartile of some independent variable (dividend yield, earnings yield, and so on). Perhaps my tables did not make this methodology as clear as it should have, since I was mixing percentiles (of the independent variable) and means (averages of all dependent values that had independent values falling with the quartile range). I concur that the median and mean agree for normal data and thank Mr. Alves for pointing out that using the terms interchangeably, especially given that the mean and median are not necessarily equal for nonnormal distributions, is imprecise.
Editor's note: For a discussion of averages versus medians, see John Ehlers' March 2005 S&C article, "What's The Difference?" (https://store.traders.com/stcov232whdi.html).
Originally published in the May 2008 issue of Technical Analysis
of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright
2008, Technical Analysis, Inc.