QUANTITATIVE METHODS
Using The Fortune Chart
Predicting Market Data Using The Kalman Filter
The Kalman filter is a two-stage algorithm that assumes there is a smooth trendline within the data that represents the true value of the market before being perturbed by market noise. Can this filter be used to forecast stock price movements?
Figure 1 on page 46 shows daily opens for one year (252 days) of Ford Motor Co. (F). According to modern financial engineering principles, market data such as this is considered to be Brownian motion, which means that the daily price changes form a white-noise process. White noise is a random process in which consecutive values are independent of each other, among other things, which means that each day, a price increase is just as likely as a decrease. In reality, it is not uncommon for a particular market item to have several consecutive down days or up days over a short time span. During such times, the prices are said to be correlated. The objective is to harness these correlations with a Kalman filter so you can forecast price movements.
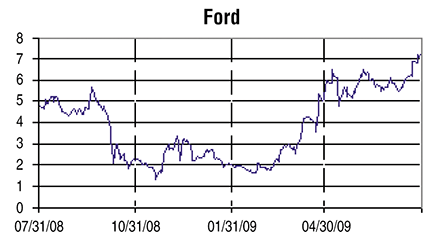
Figure 1: OPEN PRICES. On this daily chart of Ford Motor Co. (F) you can see the random nature of price movements.
In a 2006 article for Stocks & Commodities, a simple linear extrapolation was employed to predict tomorrow’s price change. The prediction was then used to calculate the alpha statistic, which compares the predicted price change to a recent average of price changes. Relatively large, positive values of alpha indicate a long position, and relatively large negative values indicate a short one. This procedure was backtested on a random selection of stocks and indexes to test its effectiveness. The indicated positions were taken, closed out the next trading day, and all profits and losses were accumulated in a chart called the Fortune. Surprisingly, of the 28 items tested, 20 produced greater profits than a simple buy & hold position for the same time period.
In this article, we will expand on the previous work, replacing the simple one-day predictor with a Kalman filter. The Kalman, as applied here, is a two-stage algorithm that assumes there is a smooth trendline within the data that represents the true value of the market item before being perturbed by market noise. In the first stage, a few previous trendline values are fit to a suitable model. It is then extrapolated to the next time value to generate a prediction and its error variance.
In the second stage, the corresponding data value is read and a new trend value is computed as a compromise between the prediction and actual data value. The compromise is based on the relative amounts of noise in the data and predictions. The filter then repeats the cycle of prediction and correction as each new data value is read.
The predicted price change and its standard deviation from the filter’s first stage are combined to produce the alpha statistic, which is used to determine buy/sell signals. A simulated trading scheme executes those signals and, as before, profits and/or losses are accumulated in the Fortune. Items are selected for simulation based on a new data property called the available profit. The ratio of the fortune to available profit defines a characteristic of the filter called its efficiency.
The next sections discuss the Kalman filter and details of the simulation method. The last sections discuss results of simulations on real stock data and offer some conclusions.