Q&A

Explore Your Options
Got a question about options? Tom Gentile is the chief options strategist at Optionetics (www.optionetics.com), an education and publishing firm dedicated to teaching investors how to minimize their risk while maximizing profits using options. To submit a question, post it on the Stocks & Commodities website Message-Boards. Answers will be posted there, and selected questions will appear in future issues of S&C.
DECAY RISK
I often hear traders discuss time decay as being a greater risk the closer to expiration that an option is. But if an option costs more with greater time remaining, wouldn’t that call or put carry increased risk, relatively speaking?
What you’ve heard discussed or read about is the nonlinear nature of theta with an emphasis on at-the-money (Atm) options. Theta is a greek factor that measures the daily rate at which a call or put will lose value, all else being equal from one trading day to the next.
During an option’s last month or so prior to expiration, this greek builds its role to reduce extrinsic or time value down to zero on a daily basis. Atm options are the most sensitive to this phenomenon, as they’re made up almost entirely of time value.
With regards to this loss of value, it’s during the final month of a contract’s life that it will stand to lose the most time decay on a month-over-month basis. During this period, theta builds at an accelerating pace in order to reduce an option’s extrinsic value toward zero before backing off in the final days, but not before the lion’s share of its earlier worth is wiped out.
For the more mathematically inclined, theta for an at-the-money option can be expressed as operating at the square root of time when removing the potential impact of interest rates and dividends and keeping volatility constant. This is shown below for an Atm option over four months:
Atm August 20 call
30 days out = $1.00 per contract
Two months remaining
Atm August 20 call = $1.00 x 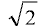 = $1.41
Three months remaining
August 20 call = $1.00 x
= $1.41
Three months remaining
August 20 call = $1.00 x 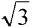 = $1.73
Four months remaining
August 20 call = $1.00 x
= $1.73
Four months remaining
August 20 call = $1.00 x 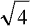 = $2.00
= $2.00
What this illustrates is accelerating time decay the closer to expiration the contract is. From four months out until three months out, the call loses -$0.27 to theta. From the third to second months out, a loss of -$0.32 is found and then -$0.41. Finally, in the final month, theta affects the option by its remaining value or a loss of -$1.00 while jumping nearly 250% from the prior month’s decay rate.
So, to answer your question, yes, a longer-dated contract does carry increased dollar risk compared to the shorter maturity. However, theta risk for two contracts over the same period is greater for the near-term contract about to expire. Other greeks such as vega (volatility risk) and delta (directional risk) will be stronger hazards to a loss in value for the longer-term contract during this period.
A MODIFIED BULL
I concentrate my portfolio on liquid, higher-priced issues like Apple (Aapl) and Google (Goog) while trading directionally. With the cost of individual options often steep, I’ve found bull and bear verticals to be my go-to strategy. Are there other spreads you would consider first or as suitable, given my preferences?
One spread that builds upon your core positioning using verticals is a modified butterfly. The modified “fly” can be legged by selling a call or put spread at a later date. That entails extra risk in the interim but does afford a profitable risk adjustment as the reward if shares cooperate.
A modified butterfly can also be executed as a spread with any option broker worth his or her salt. Either way, given your preferences, what makes the modified potentially attractive spread is the reduced cost over the vertical and flexibility as far as directional risk is concerned.
For instance, if you wish to maintain the upside profitability you’d find using a bull call spread, the modified fly can be designed with a tighter strike bear call spread in relation to a wider bull call spread. This type of modified fly is illustrated using a one-lot October 250/270/280 call fly in Aapl (Figure 1). Unlike with a regular butterfly with equidistant wings, this structure ensures some measure of upside profitability above the highest purchased strike.
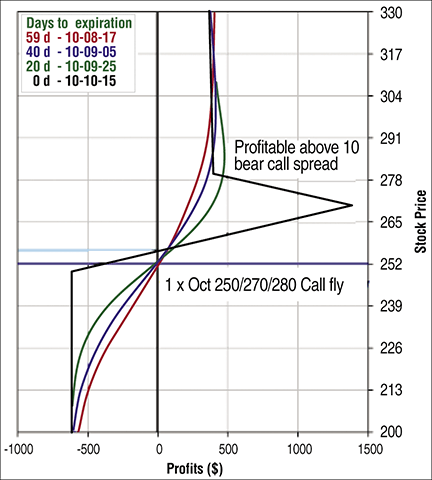
figure1: CALL FLY
SKEWED VIEW OF BULLS
Why do some stocks trade with a steepening of implied volatility the more out-of-the money the call is? In my experience, this is different from how most equity options and major indexes are priced.
This phenomenon largely boils down to volatility expectations in the underlying stock and actual supply versus demand for its options. Traders responsible for the unusual-looking skew are willing to buy higher-priced upside IV protection when selling premium by itself, such as with a buy-write, is seen as extra risky.
In most stocks, the buy-write works as a conservative means of collecting premium and reducing cost basis as shares meander technically. As such, those executing this strategy are quite happy to continue working this type of position as long as the risk to reward remains favorable.
Sometimes, however, when an issue finds sufficient bullish traction, traders realize the opportunity cost element of a buy-write’s limited upside if left unadjusted. When this attitude prevails, it removes potential supply from the pricing while premium buyers step up as the primary order flow in an effort to take advantage of those same conditions forcing sellers to back off.
Stocks that may be targeted as takeover candidates can find this type of skew, as premium sellers decide to take on a measure of risk control to prevent blowout risk. Another situation common to this IV condition is with popular growth stocks.
Growth stocks, particularly those with lesser floats, are susceptible to this abnormal skew. Traders involved with these stocks are well aware of steep and fast moves capable of pushing shares through multiple strikes before the story fades and the stock eventually corrects. In this situation, buy-writes become unattractive and short curve strategies such as short straddles and front-spreads become very difficult to manage profitably, if at all, due to negative gamma and deltas on the wrong side of directionally bullish and building volatility.
Contributing analysis by senior Optionetics strategist Chris Tyler.