May 2011 Letters To The Editor

MATHEMATICAL EXPECTATION

Editor,
I have been a follower of your magazine for quite some time, and usually read it from cover to cover as soon as it arrives in the mail. For some time I have been using an evaluation methodology similar to what Stephen Massel describes in his article, “What Can You Expect, Mathematically?” in the March 2011 issue of S&C.

I was pleasantly surprised to see the methodology I use in evaluating my trading systems described in such a good fashion, and can’t help but ask the author about the single discrepancy I have with the one described in the article. Massel describes the calculation for the reward/risk ratio as the average profit per trade/average loss per trade in dollars as an appropriate measure. I moved away from using such a measure some time ago, as it is very dependent on the price of the instrument being traded (and thus on the position size) — as the author properly states in his “Application To Your Own Trading” section. Instead, I prefer to use the payoff ratio, which is calculated as (average percentage profit per trade)/(average percentage loss per trade). Conceptually, they should be equivalent, as both of them are dividing an average profit per trade by an average loss per trade (one expressed in dollars and the other one expressed as a percentage). However, in practice, I have found that there are slight differences in the result between each approach. In some cases, the percentage calculation for the expectancy is higher and in others the absolute amount calculation is higher, as can be seen in the attached spreadsheet [click here to download —Ed.] with a set of tests runs.

Conceptually, I think there should be a preference for the expectancy calculated as a percentage, since it offers the advantage of independence to the price level of the traded instrument. Can the author offer any further insight on this?

On a side note, the article mentions that the author works in Wealth-Lab. Does he have any performance visualizer for the Wealth-Lab platform that incorporates the measures he mentions in his article?

Thanks and keep up the good work.

Jorge Dardón P.
Doral, FL

Author Steve Massel replies:

Thanks for your email. Yes, I agree, the R/R ratio in dollars is more applicable when trade size is an inherent part of the strategy, for example, when adjusting for risk. A purer method of evaluation, where risk is not adjusted, would be to use R/R as the average % gain / average % loss, as I do in such cases — and as you point out, I discuss this in the section on application to your own trading.

I have played around with mathematical expectancies (MEs) in Wealth-Lab. I have added the ME to the PerfScript code so that it is calculated and displayed as part of the standard metrics in the performance tab. I have also written an indicator that shows a rolling ME calculation based on period-to-period price moves. I would be happy to share these with you, if you would like.

Please also note that the following typo appeared in the article: The scalp system example, R/R, should have been 0.8 instead of 0.9 in order to yield an ME of 26. Unfortunately, I did not receive the spreadsheet attachment you mention.

FOLLOWUP ON MARKET INSTRUMENT FUNCTION

Editor,
The article “The Market Instrument Function” published in the December 2010 issue of S&C left me very enthusiastic about using this signals processing technique, but also perplexed as to how to do just that.

I have a background in engineering, but not in signals processing. After reviewing the “mathematical discussion” section several times, I still do not understand how to compute the E(t-tau) device instrument function. Computing the output from the input plus device instrument function is simple, but how does one compute the device instrument function from the input and output? I am interested in an expression of the type “E(t-tau)=...”

Could the authors provide an example calculation or further reading suggestions on computing the device instrument function from the input + output?

Eric Lanoix
Vancouver, BC, Canada

Authors Aleksey Gersimov and Alexander Ershov reply:

The main purpose of our article “The Market Instrument Function” was to introduce you to the instrument function method and to show a forecast for price movement that was built by this method for such assets as Dia and Spy. In the article we showed a five-year forecast. We do not know of any other method that can build such long-term forecasts.

In the article’s sidebar titled “Mathematical discussion,” we showed that the presence of an input signal, device, and output signal is always equivalent to the Fredholm equation of the first type. This part of the article is related to the problem definition but not to its solution. It is a universal mathematical description of any problem, in which the device transforms an input signal into an output signal.

For those who are interested in the solution to the problem, the following explanation is a method that makes it possible to determine the instrument function.

Consider the function , the price history, as an input signal; and the function , the future movement of prices, as an output signal. All the factors influence the pricing we describe with a market instrument function . According to our article, the detailed description is equivalent to the Fredholm equation of the first type:

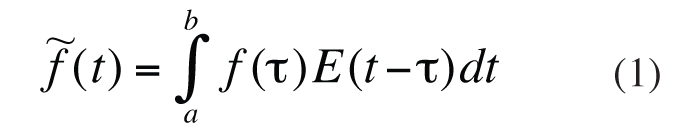
It is clear that if we know the instrument function, we can always determine the function — the future movement of prices — from equation (1). To determine , we can divide the history of the price movement into two parts and consider one of them as the past and the second one as the future. In this case, in equation (1), only one unknown function is left: function . Our aim is thereby reduced to solving the Fredholm equation of the first type relative to the equation kernel .

This equation is of a convolution type. That’s why we can apply the Fourier transform to equation (1), as follows:

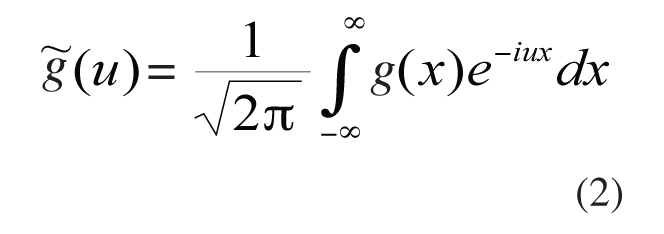
However, according to the convolution theorem, Fourier transform of convolution is a multiplication of Fourier integrals−appropriate functions; thus, we get:

where:

Thus, by means of the Fourier transform, we managed to reduce the solution of the original integral equation (1) to the solution of the algebraic equation (3) for representing the desired solution. The solution of the latter equation has the form:

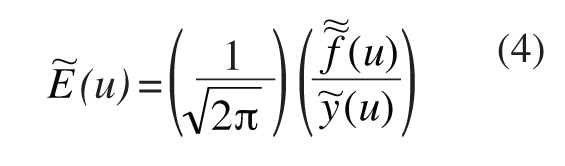
where the function must belong to the space L₂(−∞,∞).

By that, the representation of the original integral equation solution turned out to be expressed through representations of the given functions — input and output signals.

The solution itself can be expressed by means of the inverse Fourier formula:

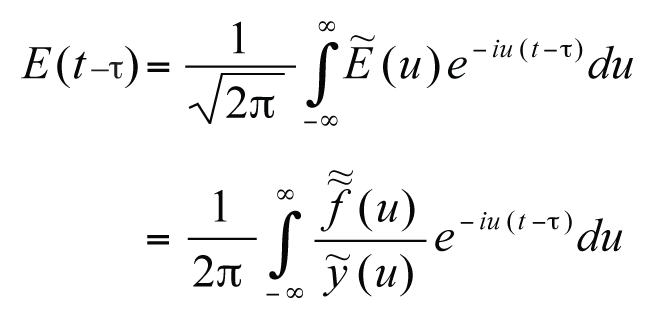
Herewith, the limits of integration in equation (1) can be determined from the maximum of the correlation function of the functions and .

Please note that the dependence of the market instrument function on the difference of t and means the presence of temporal shift between the functions and .

Finally, here is a list of further reading readers may find useful:

• Hackbusch, Wolfgang [1995]. Integral Equation: Theory And Numerical Treatment, Birkhäuser Verlag.
• Jerri, Abdul J. [1985]. Introduction To Integral Equations With Applications: Pure And Applied Mathematics, Marcel Dekker.
• Kanwal, Ram P. [1996]. Linear Integral Equations, 2nd edition, Birkhäuser.
• Polyanin, Andrei D., and Alexander V. Manzhirov [2008]. Handbook Of Integral Equations, Crc Press.
• Porter, David, and David S.G. Stirling [1990]. Integral Equations: A Practical Treatment, From Spectral Theory To Applications, Cambridge University Press.
• Smithies, F. [2009]. Integral Equations, Cambridge University Press.

NEW FORMAT FOR TRADERS’ TIPS

Editor,
As a long-time subscriber and reader of your magazine, I enjoy your magazine and get a lot of good trading ideas from it. However, I dislike the new format for the Traders’ Tips column. I don’t like that you no longer print the code but instead direct readers to your website or to the contributor’s website for the code. When I tried going to your website for the code, I found it was down, so I wasn’t able to obtain the code when I wanted to use it. In addition, at some of the software developers’ websites, it can be very difficult to find the current code or it is not posted there.

I liked your old format where the code was printed in the monthly magazine, so that I can be sure I’ll have a copy of the code available. Please go back to printing the code in each month’s hardcopy edition.

Paul

Thank you for writing. We discontinued printing all the code (for the most part) in the Traders’ Tips section because of the space it took and because printed code just isn’t very useful, given the difficulty (or impossibility) of accurately keying in long code lists. Since most readers want to copy and paste the code anyway from a web page, we opted to move the code online and started printing mainly the commentary from the Traders’ Tips contributors, producing a more condensed section in the printed magazine, with some exceptions. (In this issue, we’ve included some code because the code listings were short.)

In any case, we regret any frustrations this change may cause some readers. We will continue to print code in articles and in the Letters section.—Editor

METASTOCK CODE FOR CUP FORMATIONS

Editor,
In “Identifying Cup Formations Early” (S&C, April 2011), I believe there is an error in the first line of the MetaStock formula given in the article:

{Basic Definitions}
semicupperiod:=LastValue(Max(BarsSince(C>=LastValue(C*parameter)),1))+1;

I get the following alert at C*: “This is not a recognized name, constant, or operator.” I don’t know what to change it to or even what that means. Can you help?

Bob Robertson

Author Giorgos Siligardos replies:

There is no error in the code. The basic code segment is just a part of the “S&C – IsSemiCup” indicator. You are getting the error because you input only part of the indicator. The indicator is the “S&C – IsSemiCup” indicator, and the Basic code must be inserted in the line that reads <insert BASIC CODE here>.

Please review the article and also find the entire code listing at the S&C website in the Subscriber Area at: https://technical.traders.com/sub/Codes/2011/042011Siligardos.asp. [To navigate to the Subscriber Area, go to S&C’s homepage at www.Traders.com, click on “Stocks & Commodities,” and click on “Subscriber’s Area.” You will need to enter your last name and subscriber number, found on your magazine’s mailing label, to enter this area. Then scroll all the way down until you see the heading “S&C Article Code.” See also the S&C Traders’ Tips online at https://www.traders.com/Documentation/FEEDbk_docs/2011/04/TradersTips.html for additional code on cup formations for other software platforms.—Editor]

For your convenience, below I show the entire code set for the “S&C – IsSemiCup”:

MetaStock code
  --------------------------------------------
  S&C - IsSemiCup
  --------------------------------------------
  {Giorgos E. Siligardos, 2009}
  {Basic Semi-Cup Identification Algorithm}
  
  {parameter}
  parameter:=Input("parameter", 1, 100,2);
  FilC:=(Log(C));
  eps:=0.0000000001;
  
  {Basic Definitions}
  semicupperiod:=LastValue(Max(BarsSince(C>=LastValue(C*parameter)),1))+1;
  Ptop:=LastValue(HHV(FilC,Semicupperiod));
  Pbot:=LastValue(LLV(FilC,Semicupperiod));
  boxheight:=LastValue(Abs(Ptop-Pbot)/5);
  boxlength:=LastValue(Max(Int(semicupperiod/5),1));
  
  {Grid Nodes}
  b0:=LastValue(Cum(1)-semicupperiod+1);
  b5:=LastValue(Cum(1));
  b1:=LastValue(Min(b0+boxlength,b5));
  b2:=LastValue(Min(b1+boxlength,b5));
  b3:=LastValue(Min(b2+boxlength,b5));
  b4:=LastValue(Min(b3+boxlength,b5));
  L2:=Pbot+2*boxheight;
  L3:=Pbot+3*boxheight;
  
  {Directional Strength}
  DSX1:=Abs(Sum(Max(FilC-Ref(FilC,-1),0),2*boxlength)-Sum(Max(Ref(FilC,-1)-FilC,0),
  2*boxlength))/(eps+Sum(Max(FilC-Ref(FilC,-1),0),2*boxlength)+Sum(Max(Ref(FilC,-1)
  -FilC,0),2*boxlength))*100;
  DSX2:=Abs(Sum(Max(FilC-Ref(FilC,-1),0),3*boxlength)-Sum(Max(Ref(FilC,-1)-FilC,0),
  3*boxlength))/(eps+Sum(Max(FilC-Ref(FilC,-1),0),3*boxlength)+Sum(Max(Ref(FilC,-1)
  -FilC,0),3*boxlength))*100;
  
  {Conditions}
  isSemicup:=
  {1}(semicupperiod>=20)
  AND
  {2} (Ref(DSX1,-(b5-b2))>25)
  AND
  {3} (DSX2<25)
  AND
  {4}(Cum(If(Cum(1)>=b2, FilC>L3,0))= 0)
  AND
  {5}(Cum(If(Cum(1)>=b4, FilC>L2,0))= 0) ;
  
  LastValue(isSemicup*semicupperiod);