OPTIONS
In, At, Or Out?
Buying The Optimal Moneyness
The market is ready to make a move. You feel it. You see it. It is time to buy options. What moneyness will you choose? In, at, or out? Here’s part 1 of 2.
The first time we encounter the derivatives market, we are fascinated about the potential of big and quick profits buying out-of-the-money (OTM) options and selling them before expiration. Soon we discover that there are times when although we may be correct about the market trend, we nevertheless lose money. Even if we make money, we wonder if we could have better results using options of other “moneyness.”
In this first part of two, I will try to present in a clear and methodical way the three main forces applied to option prices when the underlying instrument moves in the options’ favor. I will explain the deficiencies of the classic sensitivity gauges — delta, vega, and theta — with regard to the practical aspects of option trading for the non-market makers, and employ the elasticity, %vega and %theta functions, for a clearer understanding of these forces.
On stock market index options
Unless stated otherwise, all options mentioned are considered European with a stock market index as their underlying. Such options are liquid (and consequently more fairly priced than simple stock options) and perfect for simple modeling purposes (due to absence of dividends and early execution concerns).
Delta to measure sensitivity
The simplest greek is delta. Delta measures the sensitivity of an option to a change in its underlying instrument. For example, a delta of 0.3 roughly means that a $1 change in the underlying results in a $0.30 change in the price of the option. In Figure 1, you can see the textbook graphs of the fair prices of European calls and puts along with their corresponding deltas. Judging from Figure 1, the in-the-money (ITM) options have absolute deltas closer to 1, which makes them closely related to the underlying, and OTM options have deltas closer to zero, so they are insensitive to small changes of the underlying.
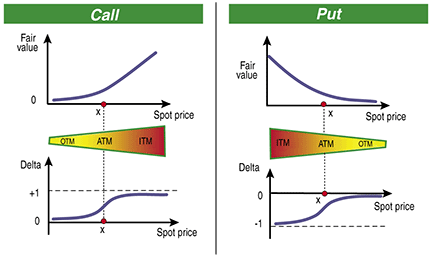
FIGURE 1: FAIR PRICES FOR CALLS AND PUTS IN ARITHMETIC CHARTS ALIGNED WITH THEIR DELTAS. The in-the-money (ITM) calls have deltas close to 1 and the ITM puts have deltas close to -1. Both the out-of-the-money (OTM) calls and puts have deltas close to zero. X is the options’ strike in the charts.