The Right One Can Mean So Much
Modeling The Market = Building Trading Strategies
by John F. Ehlers
The correct model can form the foundation for comprehensive trading strategies.
Modeling the market is important because you can build comprehensive trading strategies if your model is correct. One example of a successful model is the famous Black-Scholes model for options; a variety of options strategies have been spawned from it. Another historical model is the Hodrick-Prescott filter, which attempts to isolate the trend and cyclic components of macroeconomic data. It finds the trend by penalizing variance of the cyclic component. Once the trend is found, the implied cycle component is established as the difference between the original price and the trend. The Hodrick-Prescott is not applicable for trading, usually being applied to monthly, quarterly, and annual data samples. Philosophically, the Hodrick-Prescott has the construction of the model exactly backward. Rather than first finding the trend, I know we can measure the cyclic component of the market, and by using that, we can derive an "instantaneous" trendline.
TRENDS AND CYCLES
First, we start by assuming that our market model is made up of a trend component and a cyclic component and that we can add those two components together to synthesize a reasonable representation of the market. There are no overt constraints on these two components; the trend component does not have to be a straight line and can curve across the duration of the price chart. This is the instantaneous trendline. Similarly, the cyclic component is not constrained to have the same period. Its period or cycle length can vary across the chart also.
The cyclic period can be determined by rudimentary means such as counting the bars between successive major tops or bottoms or by sophisticated programs such as my MESA approach. Given that we know the dominant cycle, we can eliminate it by using a simple moving average (SMA) over the period of the dominant cycle. This differs from conventional moving averages by giving the freedom to change the averaging period from bar to bar.
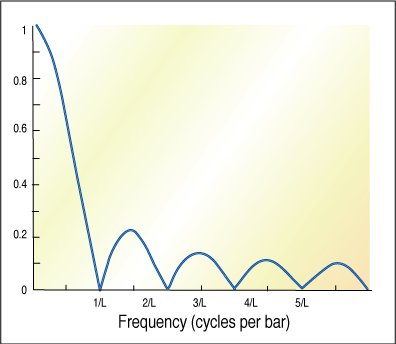
FIGURE 1: REMOVING THE CYCLIC COMPONENT. A simple moving average exactly removes the dominant cycle component and its harmonics and passes lower-frequency components....Continued in the August issue of Technical Analysis of STOCKS & COMMODITIES
Excerpted from an article originally published in the August 2006 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 2006, Technical Analysis, Inc.
Return to August 2006 Contents