CLASSIC TECHNIQUES
Beautiful Pictures
Fibonacci-Based Fractal Form And Elliott Waves
by Robert R. Prechter Jr.
The stock market is a tapestry of mathematical relations governed by Fibonacci number ratios. Here's a look at how you can apply Elliott waves to find these ratios, from a master Elliottician.
Mathematicians recognize that the stock market is a fractal, but they believe it is formless. They allow only that the irregularity of fluctuation is the same regardless of scale. R.N. Elliott observed that the stock market is a specific fractal and named it the wave principle. As defined in The Wave Principle Of Human Social Behavior (1999), the stock market is a robust fractal, meaning that it has certain specificities of form as well as quantitative variation.
Figure 1 shows an idealized Elliott wave to one, two, and three iterations. Observe that the waves in each relative position look alike regardless of size. Although this diagram is necessarily rigid, actual waves vary considerably in extent and duration. Are quantitative variations random, or do they display recognizable mathematical properties? This article investigates whether there is quantitative specificity between a wave and its same-number component.
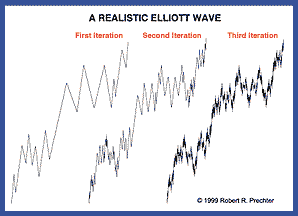
Figure 1: Elliott waves. Here you see the first, second, and third iterations.
Figure 2 displays the Dow Jones Industrial Average (DJIA) from its Depression low in 1932 through its all-time high in 2000, an advance that is labeled wave (V). Its components are labeled in Elliott wave form: I, II, III, IV, V. The final advance, surrounded by a box, is similarly labeled 1, 2, 3, 4, 5. From graphs such as this, most people would not observe how much the subdivisions of wave (V) are like those of its wave-V component.
...Continued in the September 2003 issue of Technical Analysis of STOCKS & COMMODITIES
Excerpted from an article originally published in the September 2003 issue of Technical Analysis of STOCKS & COMMODITIES magazine. All rights reserved. © Copyright 2003, Technical Analysis, Inc.
Return to September 2003 Contents