Winning Percentage Of A Trading System

by Oscar G. Cagigas

The winning percentage is a critical statistic that can influence the speed at which your capital grows. Find out how you can apply it to your trading system.

When developing a trading system, the tendency is to select a particular approach that suits your personality. With this in mind, you can develop a system with a high percentage of winning trades or one with a lower winning percentage, depending on what works best for you. A typical example is a trend-following approach. These systems usually have a winning percentage of 40–50%. Given that it is a system with a good positive expectancy, it doesn’t matter whether this system has a high winning percentage.

Developing a system based on expectancy and opportunity is popular. However, the reality is that the winning percentage is a critical statistic that influences the speed at which your capital grows. In this article, I will demonstrate this with a couple of examples.

From a Kelly perspective
Suppose we have two different systems. Both have an expectancy of 50 cents per dollar risked. The first system has a winning percentage of 40%; it is a typical trend-following system. The second system has a winning percentage of 90%. It is a typical profit-taking system that takes frequent, small profits.

Both systems have the same expectancy equal to $0.50. Using the expectancy formula, we can deduct the win/loss ratio or payoff ratio of the systems. Expectancy can be calculated as:

          Expectancy = (1+B)*P-1

where B is the W/L ratio and P is the winning percentage.

         System 1 (40% winning trades)
         Exp = (1+B) * P - 1 
         0.5 = (1+B) * 0.40 - 1

If you solve for B, you get B = 2.75.

In this typical trend-following system, there is a high win/loss ratio (2.75) and a low winning percentage (40%). Now let’s see what happens with system 2:

         System 2 (90% winning trades)
         0.5 = (1+B) * 0.90 - 1

Solving for B results in B = 0.67.

This second system sells when there is a small benefit so there is a low win/loss ratio with a very high winning percentage.

So we have two systems with the same expectancy but different characteristics. In Figure 1 we see a summary of the characteristics of these two different systems.

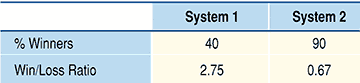
Figure 1: SAME EXPECTANCY, DIFFERENT CHARACTERISTICS. Here you see the percentage of winners and the win/loss ratio of both systems.

Now, I am going to use the Kelly approach to calculate the optimal fraction to be invested in each system. In doing this, assume a Bernoulli distribution of trades (same amount for all winners, same amount for all losers), which is not the case in trading, but ignore that for a moment to see what happens. The approach allows you to estimate the optimal percentage of your stake to risk in the next trade. As you already know the expectancy, you can calculate the optimal f by dividing the expectancy by the win-loss ratio:

         System 1
         f = exp/B = 0.5/2.75 = 18%

         System 2
         f = exp/B = 0.5/0.67 = 75%

Although both systems have the same expectancy, the second is clearly better in terms of optimal f. In the first system you should risk 18% of your trading capital in the next trade, while in the second you should risk as much as 75% of your stake in the next trade. If you take that big risk in the second system, it is because you are 90% sure that the next trade is going to be a winner.

...Continued in the April issue of Technical Analysis of Stocks & Commodities