END OF AN ERA
Editor,
Jonathan Hoenig's article ("The Rucker Park Of Capitalism," S&C, October 2000) is not dramatic enough! As a trader on LIFFE for 12 years, nine of those as a local, I know only too well how hard it is to transition from pits to screen.
Traders in Chicago have no time to waste. It is refreshing to read that most are at least attempting to learn how to screentrade. When I visited the Windy City two years ago, I was amazed at the head-in-the-sand mentality I encountered. I hope that reality is now setting in and that most traders will be able to continue their careers on the screens.
J.A. Fullick, via E-mail
TIME SERIES FORECAST INDICATOR
Editor,
I've subscribed to S&C for five or six years, and the magazine has been a key part of my education. I think the articles on trading psychology are at least as important as the technicals.
I've been searching for an Internet site that offers intraday charts (real-time or delayed) with the time series forecast indicator. I find this indicator to be one of the best available (at least for me), yet it seems impossible to find, even after many hours of hunting with the help of various search engines.
Could you ask your readers whether anyone knows of a site for stocks and/or futures that offers the time series forecast indicator?
Keep up the great work. I always look forward to the next issue.
Dave Boucher, via E-mail
MetaStock offers the time series forecast indicator and other software
may as well. This is not an indicator commonly found on free Website charting
services.-- Editor
EVIDENCE NEEDED
Editor,
I must admit, I concur with Brooks Rimes (Letters to S&C, September 2000), who questioned the place of astrology in technical analysis. I have never seen evidence to demonstrate the validity of astrology -- that is, enough evidence to stand up to statistical analysis for validity. I try to keep an open mind, but I would like to see evidence.
A year ago, I ran a test on more than 60 full moons (Figure 1). It seemed the most likely approach; the moon is close enough to cause tides, and there are rumors that people do crazy things during the full moon. The result, based on more than 60 full moons, is summarized in Figure 1. Chi-squared tests showed the difference from pure chance is insignificant.
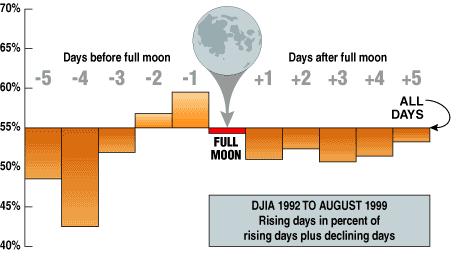
FIGURE 1: FULL MOON VS. RISING DAYS IN THE DOW JONES INDUSTRIAL AVERAGE. A study of 60 full moons against the action of the stock market shows no significant correlation statistically.
On another topic, John Ehlers' article ("Squelch Those Whipsaws,"
S&C, September 2000) was interesting but useless to anyone who doesn't
understand EasyLanguage code! Isn't it possible to explain the formulas
in highschool algebra? Every computer program starts with the formulas.
(I know; I've written scores of programs.) Here's an example from the EasyLanguage
table: I'm mystified by the meaning of "Compute a differential
phase, resolve phase wraparound, and limit delta phase errors." I'd
be willing to bet a good portion of your readers are just as mystified.
I'm writing a book on simplified statistics and will send you a draft for review and suggestions. It's going down the backstretch -- 20 chapters finished, only a few on probability left.
Keep up the good work. I clip articles from every issue.
Arthur Merrill
Haverford, PA
For many years, Art Merrill published Technical Trends, the only
digest that tracked statistically significant stock market indicators.
He also wrote many superb articles for S&C. It's good to hear from
a true pioneer of technical analysis. I look forward to seeing his book.
As for presenting the algebra, whenever we have the time, we translate the code into straight math or Excel.-- Editor
CORRELATION ANALYSIS
Editor,
The July 2000 article in S&C by Alex Saitta, "Commodities And The Inflation Rate," was of great interest to me. I had previously completed a research project using correlation analysis to develop several mutual fund bond trading systems. I used some of Saitta's articles in your fine journal as a starting point for my research. As a result of this work, I have become a devoted fan of correlation analysis. This piece was a nice followup, and I was pleased to see the section advocating the use of the deviation of the correlation coefficients from the average correlation.
There is one aspect of Saitta's July article that I would like to have clarified. The study begins with a calculation of the correlation between the prices of commodities and the inflation rate. Following the example in the sidebar, we see that the price of gold is used with the change in the Consumer Price Index (CPI). This results in a correlation coefficient that compares an absolute price series with a rate-of-change series, since the inflation rate is actually a year-over-year rate of change in the CPI.
To demonstrate the apparent incongruity, I recalculated various correlation coefficients using gold and the CPI and produced very different results. Using the price of gold and the actual CPI for the same 1997 period yielded a correlation of negative 0.873. Using the annual change in the price of gold with the annual inflation rate yielded a correlation of 0.694. This seemed somewhat useless; I don't think the annual change in gold is meaningful. Therefore, I moved to a monthly rate of change in the two series, which produced a coefficient of only 0.290.
Admittedly, the inflation rate is the number that everyone watches. The actual CPI is normally a constantly rising value. But I have read that correlation analysis is only useful if the relationships being tested make sense. It seems this tenet includes using data that is comparable or measures something in the same way. What am I missing? Is there a guideline to tell if it is appropriate to calculate the correlation of seemingly different data in this manner?
Lyndon Turner, via E-mail
Alex Saitta replies:
The level of the inflation rate and the level of annual percentage change of the Consumer Price Index are the same thing. In both cases, I compared the level of the commodity with the level of the inflation rate. I also compared the level of gold with the level of the inflation rate, which happens to be a change in the CPI. I was not comparing the level of gold with the changes in the inflation rate. That wouldn't make sense to me.
To the bond holder who receives a fixed coupon every year, the rate of inflation, or the rate the CPI rises, is important. If his coupon is $8 on a $100 bond, he is earning 8%. If the CPI is rising 5% in one year, his purchasing power increases by 3%. If the CPI rate falls to 2%, his real gain is 6% (8% coupon minus 2% inflation).
As to the rate of change of gold, I think it can be useful at times.
ERRATA: ENHANCED FUND SWITCHING
Editor,
I enjoyed Jack Singer's article in the October 2000 issue of S&C ("Enhanced Fund Switching"), but I have a couple of comments about Figure 4 and the TechniFilter Plus code. The article describes determining the 104-week highest high (HH) and lowest low (LL). Instead, Figure 4 and the TechniFilter Plus code seem to suggest that a 50-week time period is being used for all calculations except relative strength. Also, unless I have made a calculation error, the RS From Low column in Figure 4 should probably be based on values in the Close column and in the Lowest column, yet I have been unable to reproduce the values in the RS From Low column.
Steven Dubec, via E-mail
Jack Singer provided the following corrected Technifilter Plus formulas
for his article on mutual fund ranking. -- Editor
Formulas for TechniFilter Plus
[1] NAME: Close
FORMULA: C
[2] NAME: Move
FORMULA: C-Cy1
[3] NAME: %
FORMULA: ((C-Cy1)/c)*100
[4] NAME: High
PARAMETERS: H,50
FORMULA: ((&1)M&2)
[5] NAME: % frm high
PARAMETERS: H,50
FORMULA: ((c-((&1)M&2))/((&1)M&2))*100
[6] NAME: Rel Str
PARAMETERS: 104
FORMULA: 100*(c-cy&1)/cy&1
[7] NAME: Lowest
SWITCHES: multiline
PARAMETERS: C,50
FORMULA: [1]: (&1)m'&2
[2]: (&1)N[1] {v}
[8] NAME: % from Low
FORMULA: IF_THEN(C=[7],0,((c-[7])/[7])*100)
[9] NAME: Recovered
FORMULA: ((c-[7])/([4]-[7]))*100
[10] NAME: Relative Strength from Low
PARAMETERS: [7]
FORMULA: ((c-&1)/&1)*100
[11] NAME: StrHld
PARAMETERS: H,50,6,19,9
FORMULA: ((c-(((&1)M&2)-(T*0.12)))U1)+(((CX&3-CX&4)-TX&5)u1)
[12] NAME: EMA
FORMULA: CX28 <= L + .02
Note: Formulas [8] and [10] are effectively the same formula, however, if the close is equal to the lowest low, then a zero will appear in the column. This is for the benefit of clients, who receive the spreadsheet weekly and find it easier to read and understand.